Докажите равенство 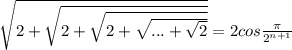
Все это равенство n радикалов
Другие вопросы по теме Алгебра
Популярные вопросы
- Наибольшее сжатие среди планет Солнечной системы имеют две планеты...
2 - Самым маленьким альбедо среди планет Солнечной системы обладает...
1 - Укажите правильное расположение объектов в порядке удаления от...
1 - В зоне жизни в настоящую эпоху находятся планеты 1) Меркурий 2)...
3 - Какая планета вращается быстрее всех вокруг Солнца? Каков её сидерический...
2 - О чём не свидетельствуют кривые А и В на графике ускоренного расширения...
3 - На каком из спутников больших планет обнаружены действующие вулканы?...
2 - На какой планете Солнечной системы обнаружены следы вулканической...
1 - Орбиты планет Солнечной системы 1) являются круговыми 2) имеют...
1 - Укажите планету, ось вращения которой почти перпендикулярна плоскости...
2
Объяснение:
Формула:
S(n) - n радикалов
Используем метод мат индукции
1) Покажем верность равенства при n=1, 2, 3
2) Предположим, что равенство верно при n=k
3) Покажем, , что равенство верно при n=k+1
Ч.т.д.