Докажите равенство. Тема является новой для меня, поэтому как можно подробнее
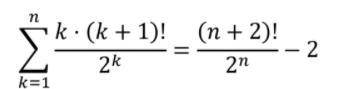
Другие вопросы по теме Алгебра
Популярные вопросы
- Какое число нужно умножить самого на себя что бы получилось 900...
1 - Пословица выражающая смысл сказки лиса и заяц...
1 - Укажите род имён существительных.мои родители самые лучшие и добрые.моего папу...
3 - Если у тебя на кухне электрическая плита и газа в доме нет значит ли это что знать...
1 - Черешня стоит 150 руб. за килограмм виноград 160 руб. за килограмм на сколько процентов...
3 - Решить по действиям. -13,9(-8,4+5,2b)-10,7(6,8-95b)-29,37b-51...
1 - Сочинение по рассказу жилина и костылина.(из рассказа кавказкий пленник)...
2 - 30 , нужна , с какими из перечисленных ниже веществ реагирует бензол: 1) озон,...
1 - Вдвух ящиках было 24 кг.лука. во втором ящике лука было в 3 раза больше, чем в...
1 - Поиск суммы от 1 до n. составить блок схему...
1
Все таки не удержусь и для начала покажу красивый без метода мат индукции, а потом уже с методом мат. индукции.
Первый .(собственно то, как, возможно, была выведена эта формула)
Обозначим сумму ряда за S:
1*2!/2 + 2*3!/2^2 + 3*4!/2^3+...+n(n+1)!/2^n = S
Рассмотрим также вс сумму S1:
2!/2 +3!/2^2 + 4!/2^3 +...+(n+1)!/2^n = S1
Тогда не трудно убедится, что
S+2S1 = 3*2!/2 + 4*3!/2^2 + 5*4!/2^3+...+(n+2)(n+1)!/2^n =
= 3!/2 + 4!/2^2+ 5!/2^3+...+(n+2)!/2^n = 2*( 3!/2^2 + 4!/2^3 +...+(n+2)!/2^(n+1) =
= 2(S1 -2!/2 + (n+2)!/2^(n+1))
То есть получаем равенство:
S+2S1 = 2S1 -2! + (n+2)!/2^n
Замечаем, что 2S1 сокращается:
S = (n+2)!/2^n - 2
Что и требовалось доказать.
Второй (метод математической индукции)
Проверим, что тождество верно для n = 1:
1*2!/2 = 3!/2 - 2
1 = 3 - 2 - верно.
Предположим, что утверждение справедливо для n = t, то есть:
1*2!/2 + 2*3!/2^2 + 3*4!/2^3+...+t(t+1)!/2^t = (t+2)!/2^t - 2
Докажем его справедливость для n = t+1
То есть нужно доказать, что:
1*2!/2 + 2*3!/2^2 + 3*4!/2^3+...+t(t+1)!/2^t + (t+1)(t+2)!/2^(t+1) = (t+3)!/2^(t+1) - 2
Нетрудно заметить, что:
1*2!/2 + 2*3!/2^2 + 3*4!/2^3+...+t(t+1)!/2^t + (t+1)(t+2)!/2^(t+1) =
= (1*2!/2 + 2*3!/2^2 + 3*4!/2^3+...+t(t+1)!/2^t) + (t+1)(t+2)!/2^(t+1) =
= (t+2)!/2^t - 2 + (t+1)(t+2)!/2^(t+1) = 2(t+2)!/2^(t+1) + (t+1)(t+2)!/2^(t+1) - 2 =
= (2+t+1)*(t+2)!/2^(t+1) - 2 = (t+3)((t+2)!/2^(t+1) - 2 = (t+3)!/2^(t+1) - 2
А значит, по принципу математической индукции, данное тождество доказано.