Докажите что выражение 4 в сороковой степени минус 1 делится на цело на 5
Другие вопросы по теме Алгебра
Популярные вопросы
- Какие отрасли получили развитие в западно сибирском районе. И...
3 - Твір «Діяльність литовських князів з династії Гедиміновичів на...
2 - Задания для практических работ 3. Составьте Составьте таолицу...
2 - Исправьте предложения 1.Его предсмертельные слова запали мне в...
1 - Составь уравнение химической реакций, протекающей при взаимодействии...
3 - Прямые PP1 и QQ1 перпендикулярны плоскости и пересекают плоскость...
2 - Серія 9 N 60 крити з поданих груп слів склади речення. Запиши...
2 - На рисунке изображены два шестиугольника.Периметр большого шестиугольника...
3 - Автомобиль алғашқы екі сағатта 50км/сағ жылдамдықпен, келесі сағатта...
2 - В электрический кофейник налили воду массой 0,4 кг при температуре...
1
выражение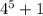 делится нацело на 5, докажем это:
делится нацело на 5, докажем это: 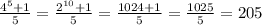
чтд
вообще, если тебе интересно, то выражение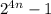 (оно же
(оно же 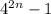 или
или 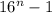 ) при
) при 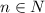 всегда делится нацело на 5
всегда делится нацело на 5