Докажите ,что уравнение х^3-х-3=0 не имеет целых корней .найдите корни уравнения х^3-7х^2+7х+15=0

1) Построим графики функци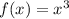й и 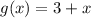- прямую, проходящей через точки (0;3), (-3;0).

На рисунке видим, что корень уравнения принадлежит промежутку (1;2), что само собой не является целым.

2) Решим данную задачку методом разложения на множители.

Произведение двух множителей равно нулю, значит

По т. Виета