Докажите, что при верно неравенсто $(2sinx +\frac{1}{cosx}) (2cosx+\frac{1}{sinx}) \geq 8$ )
и х больше или меньше пи деленное на 2

Ответы

MashaTears1 04.10.2020 08:15

Умножим левую и правую части неравенства на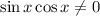 $\sin x\cos x\ne0$ и умножим отдельные множители на каждую скобку.

$(2\sin x\cos x+1)(2\cos x\sin x+1)\geq 8\sin x\cos x\\ \\ (\sin 2x+1)^2\geq 4\sin 2x\\ \\ \sin^22x+2\sin 2x+1-4\sin2x\geq 0\\ \\ \sin^22x-2\sin 2x+1\geq 0\\ \\ (\sin 2x-1)^2\geq 0$

Это верно для всех х, кроме х = πn/2, n ∈ Z

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

Тьома11 17.07.2019 21:50

Напиши уравнение оси симметрии параболы у=-х^2+2х-3...

lehayoutube 17.07.2019 21:50

Решите уравнение (5а+9)в квадрате=(5а-3)(5а+3)...

Liza111333 17.07.2019 21:40

1.решить уравнения. а) 2-3(5+2х) =6х-5; х²+11х -12=0;...

Posrednikova04 17.07.2019 21:40

Сторона треуг равна 18 а высота проведеная к этой стороне равна 22 найдите площадь треугольника...

мaкs2005 17.07.2019 21:40

Решите уравнение (3х-2)в квадрате =9х в квадрате-8х...

кококо23 17.07.2019 21:40

Объясните как находить производную для: 1) cos(2x) 2)cos(3x) 3) cos( x-(pi/3) 4) cos³(x)...

ryzhovaelena1 17.07.2019 21:40

Для приготовления 640 граммов раствора необходимо 16 граммов вещества. сколько граммов вещества необходимо взять для 240 граммов раствора?...

Даша0124 17.07.2019 21:40

Решить логарифм по основанию 2 (7-х)=6,заренее )...

Brаun 17.07.2019 21:40

Решите систему уравнений 2х+5у=13 3х-5у=-13 !...

kiki121 17.07.2019 21:40

Последовательности заданы несколькими первыми членами одна из них прогрессия укажите её 1)6 7 9 11 2) 2 4 8 16 3) 2 4 6 12...

Докажите, что при верно неравенсто )и х больше или меньше пи деленное на 2

Популярные вопросы

Докажите, что при верно неравенсто $(2sinx +\frac{1}{cosx}) (2cosx+\frac{1}{sinx}) \geq 8$ )
и х больше или меньше пи деленное на 2