Докажите, что при любом n число 2n^6-n^4-n^2 кратно 36
Другие вопросы по теме Алгебра
Популярные вопросы
- решить Есеп бойынша орнектер курастыр....
2 - Розв яжіть систему рівнянь додавання х+у=5, х-у=1...
3 - СОР по Русскому языку 6 класс 4 четверть 2 вариант...
2 - Когда впервые, по воспоминаниям мальчика, в нем чувство жалости к человеку?...
3 - Запишите область допустимых значений переменных дробей, ответ запишите...
3 - Атаулы сөйлемді тап.Дала./Бұлтты аспан.Сонау бел астында жаңа шахта құрылысы...
2 - 3. Завдання. Зміни слова так, щоб відбулося чергування голосних звуків....
1 - 1. При каких значеннях переменной, алгебраическая дробь имеет смысл2х2...
1 - 1. На каком расстоянии от собирающей линзы нужно расположить предмет,...
2 - Виразити x через y в рівняні 3x +2y = 7 4x - 8y = 6 Виразити y через...
3
Данное число 36 можно представить как 36 = 2 * 2 * 3 * 3.
Если n - делится на 3, то и произведение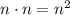 делится на 3, значит все число тоже делится на 3. Если один из чисел (n-1) и (n+1) делится на 3, то их произведение
делится на 3, значит все число тоже делится на 3. Если один из чисел (n-1) и (n+1) делится на 3, то их произведение 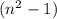 также делится на 3, тогда
также делится на 3, тогда  тоже делится на 3 и следует деление на 3
тоже делится на 3 и следует деление на 3 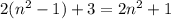 . Таким образом, данное выражение делится на 36 при любом n.
. Таким образом, данное выражение делится на 36 при любом n.
Відповідь:
Пояснення:
Для того, щоб число ділилось на 36, потрібно довести подільність на 4 и 9.
2n⁶-n⁴-n²=n²(2n⁴-n²-1)=n²(n²-1)(2n²+1)=n²(n-1)(n+1)(3n²-(n²-1))=
=(n-1)n(n+1)(3n³-(n-1)n(n+1)).
Якщо n - парне, то через множник n², весь вираз ділиться на 4.
Якщо n - непарне, то відповідно n-1 и n+1 - парні і знову все кратно 4.
(n-1)n(n+1) - добуток трьох послідовних чисел, тобто кратно 3.
Тому і 3n³-(n-1)n(n+1) - теж ділиться на 3, а отже, все кратно 9.