Докажите, что при a> 0 имеет место неравенство (x+3)(x+6)(x+2)(x+1)> 96x^2

Приведу самое оптимальное решение. Воспользуемся неравенством Коши: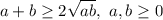

В нашем случае, x > 0, значит

Умножив все четыре неравенства, мы получим

Необходимо доказать, что:

(x+3)*(x+6)*(x+2)*(x+1)>96*x^2

При условии: x>0

Умножим первую скобку на третью, а вторую на четвёртую:

(x^2+5x+6)*(x^2+7x+6)>96*x^2

Поделим обе части неравенства на x^2 , причём каждую из полученных скобок поделим почленно на x. Поскольку x^2>0 , то неравенство не меняет знак.

Имеем:

(x+ 5+ 6/x)*(x + 7 +6/x)>96

Сделаем замену : x+6+6/x=t

(t-1)*(t+1)>96

t^2-1>96

t^2>97

Необходимо доказать , что t^2>97

Поскольку x>0 , то можно применить неравенство о среднем арифметическом и среднем геометрическом:

x+ 6/x >= 2*sqrt(x *6/x)=2*sqrt(6)

Откуда:

t= x+6 +6/x>= 6+2sqrt(6)

t^2>=(6+ 2sqrt(6) )^2=36+24+24*sqrt(6)

=60+24*sqrt(6)>60+24*sqrt(4)=

=60+48=108>97

Таким образом мы показали что:

t^2>97, а значит мы доказали , что неравенство:

(x+3)*(x+6)*(x+2)*(x+1)>96*x^2 выполняется при любом x.

Что и требовалось доказать.

Более того , мы может даже усилить данное неравенство , сделав его строгим и найти наибольшее целое число , что может усилить данное неравенство.

t^2-1>= (6+ 2sqrt(6) )^2-1=59+24sqrt(6)

(x+3)*(x+6)*(x+2)*(x+1)>=(59+24sqrt(6))*x^2

24*sqrt(6)=sqrt(24^2 *6)=sqrt(3456)

sqrt(3364) <sqrt(3456) < sqrt(3481)

58 <24*sqrt(6)<59

59+24sqrt(6) >59+58=117

Наибольшее усиление для сравнения с целым числом:

(x+3)*(x+6)*(x+2)*(x+1)>117*x^2