1. Алгебра
  2. Докажите,что многочлен принимает

Докажите,что многочлен принимает только не отрицательнве значения x²+y²+2x+6y+10​

phon1 phon1    1   24.02.2021 19:13    1

Ответы
kall4 kall4  26.03.2021 19:13

Объяснение:

x²+y²+2x+6y+10​>=0

x²+2x+1+y²+6y+9>=0

(x+1)²+(y+3)²>=0

(x+1)²>=0 (y+3)²>=0

Любое отрицательное число в квадрате будет положительным =>

При x принадлежит (-Б;+Б), уравнение x²+y²+2x+6y+10​>=0 больше или равно нулю => x²+y²+2x+6y+10 не может быть меньше нуля..

ч.т.д.

ПОКАЗАТЬ ОТВЕТЫ
НадеждаКрасюкова НадеждаКрасюкова  26.03.2021 19:13

    x^{2} +y^{2} +2x+6y+10=

=x^{2} +y^{2} +2x+6y+1+9=

=(x^{2} +2x+1)+(y^{2}+6y+9)=

=(x+1)^{2} +(y+3)^{2}

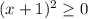1)  (x+1)^{2} \geq 0  при любом значении переменной x квадрат выражения принимает только не отрицательные значения

2)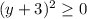  (y+3)^{2}\geq 0  при любом значении переменной 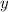y квадрат выражения принимает только не отрицательные значения

3)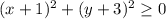  (x+1)^{2} +(y+3)^{2}\geq 0  многочлен, состоящий из двух  не отрицательных выражений, принимает только не отрицательные значения.

Доказано.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
rasulid04 rasulid04  06.04.2020 21:46
0,3,8,15,24 нужно найти алгоритм...
Nikaslavnikova Nikaslavnikova  06.04.2020 21:46
Найдите все целые решения неравенства 4x^2-8x+3 0...
Tanecka2501 Tanecka2501  06.04.2020 21:45
Назови пару чисел, являющийся решением уравнения 4x-y=12ответ: (-1;12)(0;-12)(1;4)(0;12)(4;0)​...
alanka280606 alanka280606  06.04.2020 21:44
При каких значениях a следующие неравенства сводятся к квадратным решите 543....
okszav okszav  06.04.2020 21:44
Решить неравенства 1/3x^2+3x+6 0 , − x^2 +5x −16 0, x^2 −6x 0, x^2 − 4 ≥ 0...
vlad2065 vlad2065  06.04.2020 21:43
У выражение1/x(x+1)+1/(x+1)(x+2)+1/(x+2)(x+3)+1/(x+3)(x+4)+1/(x+4)(x+5) . На фото номер 932...
evenen evenen  06.04.2020 21:42
найдите допустимые значения букв входящих в дробь а)4/хб)m-n/m+3в)-3/p^2-1г)n/n^2+4​...
Larakf Larakf  29.09.2019 06:02
Найдите площадь прямоугольника, если известно, что сумма длин двух его смежных сторон равна корень из 14, а их разность корень из 10 см...
ersultanplay ersultanplay  29.09.2019 06:02
Алебра 7 класс 0,(6)×0,(4) с решением на бумажке...
20софа05 20софа05  29.09.2019 06:02
Метод подстановки (линейное и квадратное) {d+y=7 {d⋅(d+y)=14 d= y= можно без решения...

Популярные вопросы