Докажите ,что касательные проведённые через точки графика функции
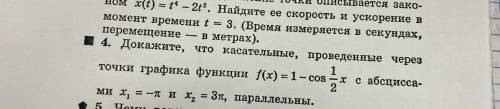
Другие вопросы по теме Алгебра
Популярные вопросы
- Выписать из сказки Конёк-Горбунок 7 простых предложений...
3 - Как называються эти 2 молекулы этилена...
3 - Сколько будет 187*6+697-156*6...
2 - На высоте 3 км термометр показывал 2°С. Какая температура была...
1 - укажи Какие из перечисленных материалов используются в строительстве...
2 - Укажите верную запись десятичной дроби «семь целых пять десятых»...
3 - 1-тапсырма. Төмендегі сұрақтарға жауап беріңіздер. 1. Сенімхат...
3 - Отметь автора поэмы «Искандер» об А. Македонском. ответы:И. ЕсенберлинШ....
2 - 2 Make a poster for a film. Follow the steps in the project checklist....
3 - На рисунке приведены примеры строения нервной системы беспозвоночных....
3
f(x) = 1 - сos 1/2x ; x1=-π ; x2= 3π
Доказать, что касательные параллельны.
1) Уравнение касательной имеет вид y=kx+b
2) k = f ′(x₀)
3) f ′ (x) = ( 1 - cos1/2x ) ′ = 0 - (1/2x) ′ * (-sin1/2x) = 1/2sin*1/2x
4) k1 = f ′ (-π) = 1/2sin * ( 1/2*(-π)) = -1/2sin*π/2= -1/2
5) k2 = f ′ (3π) = 1/2sin*1/2*3π = 1/2*sin3π/2=-1/2
Таким образом, угловые коэффициенты двух касательных одинаковые, так как:
k1 =-1/2 и k2=-1/2
Значит прямые, которые являются касательными параллельные прямые.