Докажите, что функция является чётной
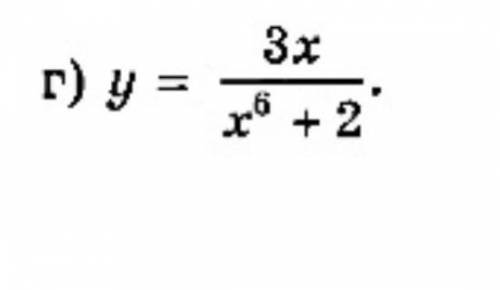
Другие вопросы по теме Алгебра
Популярные вопросы
- Українська література 10 клас, твір: Impromptu phantasie , До ть, будь ласка❤️...
2 - Ребят по английскому. вроде не сложно только смекалка нужна ,ну и переводчик...
1 - Сочинение рассуждение:какими качествами должен обладать рыцарь...
1 - Желательно с пояснением Дам максимально кол во !!...
2 - с заданием 1 класс 5*35:53:14:2 Я немогу решить не понимают ...
3 - умоляю это сор по естествознанию...
2 - Кільце з мідного дроту масою m =10 г розміщене в однорідному магнітному полі...
1 - В однорідному магнітному полі з індукцією B = 0,5Тл обертається з частотою ν...
3 - Мәтін мазмұны бойынша жоспар құрып жаз.Әр бөліктегі тірек сөздерді анықта.Жоспарда...
1 - Дано конус. Н відноситься до L, як 4:5. Об єм=96П см^3. Sповне знайти....
1
y = 3x/(x⁶ + 2)
Доказать, что y (x) - чётная функция
Доказательство:
• Функция является чётной, тогда и только тогда, когда:
y (-x) = y (x)
А нечётной, если:
y (-x) = -y (x)
• Проверяем:
y(-x) = (3 • (-x))/((-x)⁶ + 2) = -3x/(x⁶ + 2) = -(3x/(x⁶ + 2)
• Получается y (-x) = -y (x), ⇒ функция является НЕЧЁТНОЙ, а не чётной