Докажите ,что дробь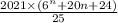
при любом натуральном "n" есть целое число ​

Достаточно показать, что выражение в числителе 6ⁿ + 20n + 24 при любом натуральном n кратно 25. Тогда дробь есть целое число. Докажем индукцией по n. При n = 1 выражение 6ⁿ + 20n + 24 = 50 = 2*25. Пусть это выражение кратно 25 при произвольном n. Покажем, что тогда и выражение 6ⁿ⁺¹ + 20(n + 1) + 24 кратно 25. 6ⁿ⁺¹ + 20(n + 1) + 24 = 6*6ⁿ + 20n +20 + 24 = 6ⁿ + 20n + 24 + 5*6ⁿ + 20 = 6ⁿ + 20n + 24 + 5(6ⁿ + 4). Число 6ⁿ + 4 оканчивается нулём, поэтому кратно 5, значит выражение 5(6ⁿ + 4) = 25k кратно 25. Член суммы 6ⁿ + 20n + 24 кратен 25 по предположению индукции, значит всё выражение 6ⁿ⁺¹ + 20(n + 1) + 24 кратно 25, отсюда следует кратность 25 выражения 6ⁿ + 20n + 24, а значит дробь 2021*(6ⁿ + 20n + 24)/25 есть целое число.