Докажите,что число (√2-1)в сотой степени можно представить в виде √m+1-√m,где m натуральное число.
Ответы
Если в числе 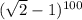 раскрыть 100-ую степень по биному Ньютона, то получится сумма слагаемых вида
раскрыть 100-ую степень по биному Ньютона, то получится сумма слагаемых вида 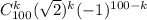 по k от 0 до 100. При четных k эти слагаемые будут натуральными числами, а при нечетных k они имеют вид
по k от 0 до 100. При четных k эти слагаемые будут натуральными числами, а при нечетных k они имеют вид 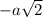 , где а - натуральное. Значит,
, где а - натуральное. Значит, 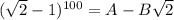 , при некоторых натуральных
, при некоторых натуральных 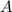 и
и 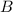 . (для решения задачи нет нужды их явно вычислять). Опять же из бинома Ньютона понятно, что тогда
. (для решения задачи нет нужды их явно вычислять). Опять же из бинома Ньютона понятно, что тогда 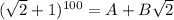 , т.к. в нем будут те же слагаемые, только все со знаком плюс. Перемножив эти два соотношения, получим
, т.к. в нем будут те же слагаемые, только все со знаком плюс. Перемножив эти два соотношения, получим 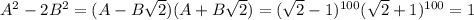 , то есть
, то есть 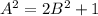 . Поэтому, если положим
. Поэтому, если положим 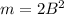 , то получим, что
, то получим, что 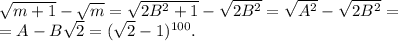
ПОКАЗАТЬ ОТВЕТЫ
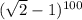 раскрыть 100-ую степень по биному Ньютона, то получится сумма слагаемых вида
раскрыть 100-ую степень по биному Ньютона, то получится сумма слагаемых вида 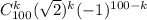 по k от 0 до 100. При четных k эти слагаемые будут натуральными числами, а при нечетных k они имеют вид
по k от 0 до 100. При четных k эти слагаемые будут натуральными числами, а при нечетных k они имеют вид 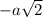 , где а - натуральное. Значит,
, где а - натуральное. Значит, 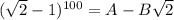 , при некоторых натуральных
, при некоторых натуральных 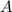 и
и 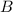 . (для решения задачи нет нужды их явно вычислять). Опять же из бинома Ньютона понятно, что тогда
. (для решения задачи нет нужды их явно вычислять). Опять же из бинома Ньютона понятно, что тогда 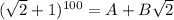 , т.к. в нем будут те же слагаемые, только все со знаком плюс. Перемножив эти два соотношения, получим
, т.к. в нем будут те же слагаемые, только все со знаком плюс. Перемножив эти два соотношения, получим 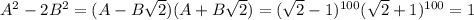 , то есть
, то есть 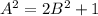 . Поэтому, если положим
. Поэтому, если положим 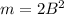 , то получим, что
, то получим, что 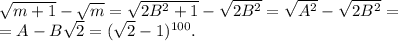
Другие вопросы по теме Алгебра
Популярные вопросы
- 3. Тип территориального устройства Речи Посполитой, мера самостоятельности...
1 - Порівняння властивостей провідників, діелектриків і напівпровідників....
2 - Билет № 21) Напишите молекулярные и ионные уравнения реакций между:а) HBr...
2 - Найдите площадь трапеции по данным на рисунке...
1 - Полная механическая энергия пружинного маятника увеличилась в 3 раза. Во...
2 - № 7. Определите вид подчинения придаточных предложений.Уже поздней весною,...
3 - Знаю, во тупой, но тем не менее вас ответить если не сложно. Дорогие мои...
1 - Кто же был прав, Рэлей и Джинс или Вин? Почему расчёты этих учёных в конце...
2 - Почему спектры атомов явились причиной создания квантовой механики ?...
1 - Як жили люди в середньовичній Європі ...
2