Докажите , что : a²+b²> (a+b)²÷2
Памагиииттеее

Объяснение:

a²+b²>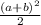

Объяснение:

a²+b²>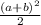 домножим обе части неравенства на 2:

2a²+2b²>(a+b)² применим формулу сокращённого умножения к квадрату суммы:

2a²+2b²>a²+2ab+b² вычтем правую часть неравенства из левой:

2a²+2b²-a²-2ab-b²>0

a²-2ab+b²>0 по формуле сокращённого умножения получим:

(a-b)²>0 квадрат всегда положительный, значит неравенство верно.