доказать неравенство : Дано x,y,z >= 2;
Доказать :
(x³+y)(y³+z)(z³+x) >= 125xyz
Популярные вопросы
- Треугольник abc-равнобедренный ab-основание,cm-медиана .угл a=50 градусов,...
2 - Как будет слово сини в единственном числе?...
3 - Найдите стороны прямоугольника если его площпдь равна 250см одна сторона...
2 - Зная широту точек, определите, какая расположена дальше всего от экватора...
2 - 1-2/7= один минус две седьмых равно ?...
1 - His sister (to study) english every day....
3 - Втреугольнике угол авс угол с равен 90°, угол а равен 30°, вс=2√3. найдите...
2 - Дай характеристику этим предложениям. лев спал. мышь пробежала ему по телу....
2 - Определите массу бетонной плиты , у которой 120 см длина, 50см ширина, 10...
1 - Файл размером 4096 байт передаётся через некоторое соединение со скоростью...
3
Без ограничения общности положим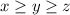 . Пусть
. Пусть 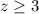 , тогда
, тогда 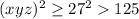 и
и 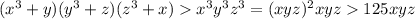 .
.
Пусть теперь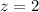 . Тогда имеем
. Тогда имеем 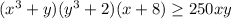 . Если
. Если 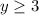 , то
, то 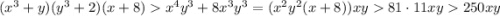 .
.
Пусть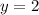 . Тогда если
. Тогда если 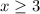 , то
, то 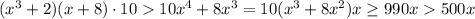 . Наконец, при
. Наконец, при 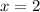 :
: 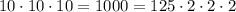 .
.