1. Алгебра
  2. Доказать неприводимость над

Доказать неприводимость над полем \mathbb{q} многочлена
x^6+x^5+x^4+x^3+x^2+x+1 по критерию эйзенштейна

artemalashev artemalashev    2   06.01.2020 21:42    2

Ответы
SaBzZiRo SaBzZiRo  10.10.2020 23:56

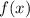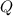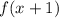Если f(x) приводим над Q, то f(x+1) также приводим над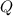 Q

(a\in Q=(a+1)\in Q\\ a\notin Q= (a+1)\notin Q)

f(x+1)=(x+1)^6+...+(x+1)+1=\dfrac{1*((x+1)^7-1)}{x+1-1}=\dfrac{(x+1)^7-1}{x}=\dfrac{C_7^0x^7+C_7^1x^6+...+C_7^6x+C_7^7-1}{x}=C_7^0x^6+C_7^1x^5+...+C_7^6\\ C_7^k=\dfrac{7!}{(7-k)!k!}=\forall k=\overline{1,6}\: \:\:C_7^k \:\vdots \:7;\:\:C_7^0=\dfrac{7!}{7!0!}=1=HOD(C_7^0;7)=1\\ C_7^6=\dfrac{7!}{6!1!}=7,\:7^2=49,\:HOD(C_7^6;49)=1

То есть существует неприводимый над Q элемент, равный 7, удовлетворяющий критерию Эйзенштейна для f(x+1). Значит f(x+1) неприводим над Q. Тогда и f(x) неприводим над Q.

Доказано.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ася766 ася766  19.05.2021 08:34
Выполните сложение и вычитание дробей: КАК МОЖНО БЫСТРЕЙ ​...
kuanyshqz kuanyshqz  19.05.2021 08:34
Выполните умножение и деление алгебраических дробей: ​...
Radigon Radigon  19.05.2021 08:34
-x^2+x+6 0 решить методом параболы...
Настя9474 Настя9474  19.05.2021 08:37
Розв яжіть рівнянняа) х2 – 9x = 0;​...
вика6010 вика6010  19.05.2021 08:38
Выполните сложение и вычитание дробей:1/7х + 1/х 2а/а+4 - 5а-2/16-а²​...
MaxineCaulfield2003 MaxineCaulfield2003  19.05.2021 08:38
Побудуйте графік функції у = 2x² - 4x + 2 Користуючись графіком, знайдіть : 1) проміжок спадання функції; 2) множину розв язків нерівностi 2x² - 4x + 2 ≤0...
дианакис050706 дианакис050706  19.05.2021 08:41
НАДО. буду очень благодарна ​...
Янияру Янияру  19.05.2021 08:41
Постройте график функцииy=4/x​...
anastasia3004 anastasia3004  19.05.2021 08:42
Задания: 1. При каких значениях переменной, алгебраическая дробьх+х+12имеет смысл? [2]2. Сократите дробь:14х2)[1]21. եթէ25-15a?3. Упростите выражение: 5а + Найдите значение...
viliam3486 viliam3486  19.05.2021 08:42
Алгебра решите неравенство 5 задание с ОДЗ...

Популярные вопросы