Доказать методом индукции что выражение 3^(4n-1)-25n^2-17 кратно 5
Другие вопросы по теме Алгебра
Популярные вопросы
- Указать наименьший общий знаменатель дроби 6/77 11/63 2/99...
3 - 292 найти корни уравнения а) |2x^2-3x+1|=|x^2+x-2|...
2 - Для приготовления молочного коктейля смешивают молоко с мороженым...
2 - При прямолинейном движении зависимость пройденного телом пути sот...
3 - Вариант раздельного написания не с наречием: 1. (не) выразимо прекрасный...
3 - Проверьте,,есть ли ошибки в тексте. макар чудра рассказал писателю...
3 - Вставьте артикли a, an, the если это необходимо 1.this is __ dog....
3 - Цену товара снизили на 20 %, через месяц - еще на 10 %. после после...
1 - Двигаясь с ускорением 2 м/с из состояния покоя тело путь 9 м определить...
3 - Дробь к знаменателю 48: 1\8 ,13\16 ,1\4,5\12,1\3,11\24,1\2,5\6...
2
1) База индукции: n = 1
2) Предположим что и для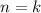 выражение
выражение 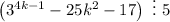
3) Индукционный переход: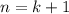
Первое слагаемое делится на 5 по предположению (пункт 2). Остальные слагаемые тоже делятся на 5, поскольку их коэффициенты делятся на 5. Значит, исходное выражение кратно 5 для всех натуральных n.