Доказать методом индукции, что:
см. 23 номер

Доказать что число 5 * 2^(3n-2) + 3^(3n-1) делится на 19

Доказательство:

1) База индукции: n = 1

2) Предположим что и при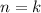 выражение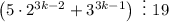

3) Индукционный переход: n = k+1

Первое слагаемое делится на 19 по предположению (второй пункт), а второе слагаемое очевидно что делится на 19, так как имеет сомножитель 19.