Доказать, что уравнение x^4 + y^4 + z^4 = 2020 не имеет решений в целых числах

По малой теореме Ферма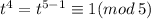 , если t не кратно 5.

Тогда, если хотя бы одно из чисел x, y, z не кратно 5, левая часть уравнения дает один из остатков 1, 2 или 3 (в зависимости от кол-ва чисел среди x, y, z, не кратных 5). С другой стороны, 2020=5*404 - кратно 5. Противоречие. Значит каждое из чисел x, y, z кратно 5.

Введем замену

Правая часть дает остаток 4 при делении на 5, а левая делится на 5. Противоречие. А значит уравнение не имеет решений в целых числах.

Ч.т.д.