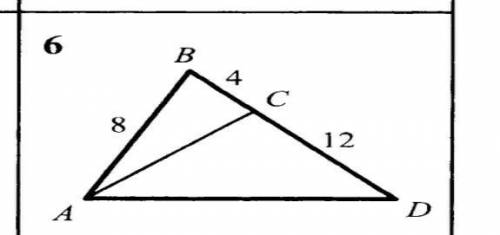
Доказать, что треугольник ABC подобен треугольнику DBA. Найдите длину отрезка AC, если AD=18
Другие вопросы по теме Алгебра
Популярные вопросы
- Как ты связываешь своё отношение к Родине с семьёй?...
3 - Характеристика Снегурочки из пьесы Островского...
1 - Выпишите предложения, в которых есть союзы тоже, также, чтобы, зато....
2 - Задание: Подчеркните логическое ударение (слово) по образцу:I can do...
1 - Почему самый высокоорганизованный является вид человек разумный...
1 - Из чисел −1; 4√; 10 и 3/10выбери числа, которые являются решением неравенства...
2 - Стоимость проезда в пригородном электропоезде составляет 234 рубля....
3 - Постройте прямую заданную уравнением y =-1/2x+3...
3 - В правильной четырехугольной пирамиде сторона основания равна 2, а...
3 - Кто мистер пидр??? за хороший ответ...
3
Для начала, давайте рассмотрим соответствующие углы треугольников ABC и DBA. В треугольнике ABC, угол A расположен напротив стороны AC, а угол B расположен напротив стороны BC. В треугольнике DBA, угол D расположен напротив стороны DA, а угол B расположен напротив стороны BA.
Из рисунка видно, что углы A и D являются вертикальными углами, а значит, они равны друг другу: A = D.
Также, углы B и B являются соответственными углами согласно задаче, и поэтому они также равны: B = B.
Таким образом, углы A и D и углы B и B равны, что говорит о подобии треугольников ABC и DBA.
Теперь давайте рассмотрим соответствующие стороны. В треугольнике ABC, сторона AC задается AB + BC, а в треугольнике DBA, сторона DB задается DA + AB.
Из условия задачи известно, что AD = 18.
Таким образом, сторона DB равна 18 + AB.
Используя данные, полученные выше, мы можем записать следующее уравнение:
AB + BC = 18 + AB.
Здесь мы используем равенство сторон треугольников ABC и DBA, так как они подобны.
Нам нужно найти длину отрезка AC. Чтобы это сделать, мы можем привести уравнение к виду, где отрезок AC находится в одной части:
BC = 18.
Таким образом, длина отрезка AC равна 18.