Доказать что модуль х-у/1-ху меньше 1, если модуль х и модуль у меньше 1

Нужно доказать, что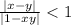

так как левая и правая части неотрицательны, это неравенство равносильно следующему (поднесем обе части к квадрату, чтобы избавиться от модуля так как |a|^2=a^2)

так как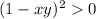 (0 не может быть потому что знаменатель не может быть равным 0, а квадрат выражения всегда неотрицателен),

то нужно доказать что справедливо неравенство

то справедливо так как (y^2-1<0; y^2<1; |y|<1) (|x|<1; x^2<1; 1-x^2>0)

(один из множителей отрицателен, другой положителен - значит и произведение отрицательное).

Таким образом цепочкой равносильных преобразований мы пришли к справедливому неравенству. Доказано