Доказать что функция 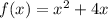
убывает на промежутке
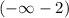
Другие вопросы по теме Алгебра
Популярные вопросы
- 1)x=2/3x+1 целая 3)x-2/3=5/6x 5)2/3y-1/3=5/9y 30...
1 - Решите уравнение: 32-х/22+2х = 14/15 ( / - дробная черта)...
3 - Какую работу нужно совершить при равномерном подъёме в воде стеклянного...
3 - Родственные узы нужно красивое определение...
2 - Сочинение на тему жизнь в глубинах космаса...
2 - 1день день день надо найти 10...
1 - Можете написать краткий пересказ гоголя-ганна(5 глава)буду...
1 - Найти значение выражения 2* 10^-1+1* +10^-2 + 1 * 10^ -4...
2 - Реформы петра 1.ответьте мне коротко...
2 - Укажите слово обозначающая схема. корень и окончание. оно обогрело,...
1
Объяснение:
Находим производную ф-ции: 2x+4
Находим критические точки, приравняв к нулю: 2x+4=0
x=-2;
Делаем небольшой рисунок и определяем знаки. Подставляем -3 вместо x и получаем -2, значит (-∞;-2) минус, ф-ция убывает. Подставляем 1, получаем 6, значит справа плюс. Если точка переходит с - на +, это точка минимума.
Производная отрицательна при х∈(-∞;-2)⇒функция убывает
Объяснение: