Добрые люди , найти условный экстремум функции
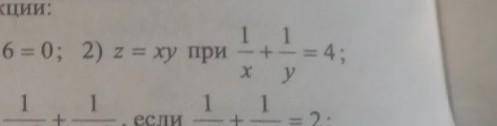
Другие вопросы по теме Алгебра
Популярные вопросы
- Чем питается жгутиканосец? ...
3 - Сравнить -5(x+1) и x-10 при x= -3...
2 - решить x-5=3x-2 , -4x-8=x-8...
3 - Відмінювання числівника 49відмінювання числівника 125...
1 - Русский язык страница 17 упражнение 9...
3 - Придумайте 5 примеров на деление дестятисных дробей...
2 - 38. Вычислите значение числового выр а) - 21 – 1,8| = c) |11:5 - 7,4 =b) |5 -...
1 - Задание следующее: нужно выписать в тетрадь путешественников, какой вклад в развитие...
1 - В треугольнике ABC BM-медиана, BH-высота, AC=25, BC=BM . Найти AH....
3 - 3. В кинотеатре 249 мест, продали 83 билета. Какая часть мест оказалась занята?4....
1
Объяснение:
z = xy, при условии 1/x + 1/y = 4
Выразим y через x:
1/y = 4 - 1/x = (4x - 1)/x
y = x/(4x - 1)
z = xy = x^2/(4x - 1)
Область определения z: x ≠ 0; y ≠ 0; x ≠ 1/4
Находим производную теперь уже функции одной переменной.
z ' = [2x(4x - 1) - x^2*4] / (4x-1)^2 = (8x^2 - 2x - 4x^2) / (4x-1)^2 = (4x^2 - 2x)/(4x-1)^2
В точке экстремума производная, то есть ее числитель, равна 0.
4x^2 - 2x = 0
2x(2x - 1) = 0
Так как x ≠ 0, то:
2x - 1 = 0
x = 1/2; y = x/(4x - 1) = (1/2) / (4/2 - 1) = 1/2
z = xy = (1/2)*(1/2) = 1/4.
В точке x = 1 > 1/2 будет z ' = (4 - 2)/(4 - 1)^2 = 2/3^2 = 2/9 > 0
Значит, при x > 1/2 функция растет.
В точке x = 1/3 < 1/2 будет z ' = (4/9 - 2/3) / (4/3 - 1)^2 = (-2/9) / (1/3)^2 = -2 < 0
Значит, при x < 1/2 функция падает.
Точка (1/2; 1/2; 1/4) - точка минимума.