Доброго времени суток решить неравенство.
за !
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишите сочинение на тему: любовь к родине....
1 - 50 преобразуйте данное целое выражение в произведение многочленов а) (х-1)(4х-6х)...
1 - 3м (квадратных) - 67 дм (квадратных)...
3 - Чтобы решить уравнение,потребовалось число 444 умножить на число 2. какое уравнение...
3 - Подберите к последнему слову в словосочетании имя существительное так, чтобы...
2 - Скакими из перечисленных веществ будет реагировать разбавленная азотная кислота:...
1 - При взаимодействии цинка с избытком раствора соляной кислоты выделился водород...
3 - Составить по выражению 20+30/ 5 и ещё краткую запись...
3 - Что такое падежные слова и смысловые вопросы...
1 - Как составить схему к предложению: он подготовился основательно: вернулся, сходил...
3
Объяснение:
Пусть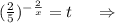
-∞__+__0,16__-__2,5__+__+∞ ⇒
t∈[0,16;2,5].
ответ: x∈(-∞;-1)U(2;+∞).