Для функции 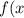$f(x)=2^x+3x$ найдите первообразную, прямая $y=5x-2$ касательная к ее графику.

Ответы

nissanbaev25 09.01.2024 22:03

Для нахождения первообразной функции $f(x)=2^x+3x$ , мы должны найти функцию $F(x)$ , такую что ее производная равна исходной функции $f(x)$ .

Итак, начнем с нахождения производной функции $f(x)$ по x.

$f'(x)=(2^x)' + (3x)'$

Рассмотрим каждое слагаемое отдельно:

1. Производная $(2^x)'$ .
Используя правило дифференцирования степенной функции, получаем:

$(2^x)' = ln(2) \cdot 2^x$

2. Производная $(3x)'$ .
Используя правило дифференцирования произведения функции на константу, получаем:

$(3x)' = 3$

Теперь объединим результаты:

$f'(x) = ln(2) \cdot 2^x + 3$

Теперь, чтобы найти первообразную функцию $F(x)$ , мы должны найти такую функцию $F(x)$ , производная которой равна $f(x)$ .

Мы уже вычислили производную функции $f(x)$ , поэтому можем записать:

$F'(x) = ln(2) \cdot 2^x + 3$

Теперь интегрируем выражение слева и справа от знака равенства:

$\int F'(x) dx = \int ln(2) \cdot 2^x + 3 dx$

Известно, что интеграл производной функции равен исходной функции, поэтому получаем:

$F(x) = \int ln(2) \cdot 2^x + 3 dx$

Далее, для упрощения интеграла, разделим его на две части:

$F(x) = \int ln(2) \cdot 2^x dx + \int 3 dx$

Интегрируем каждую часть по отдельности:

1. Интеграл $\int ln(2) \cdot 2^x dx$ .
Используя правило замены переменной, где $u = 2^x$ и $du = ln(2) \cdot 2^x dx$ , получаем:

$\int ln(2) \cdot 2^x dx = \int du$

Интеграл $\int du$ равен $u$ , поэтому:

$\int ln(2) \cdot 2^x dx = 2^x + C_1$ , где $C_1$ - произвольная константа.

2. Интеграл $\int 3 dx$ .
Интегрируя константу, получаем:

$\int 3 dx = 3x + C_2$ , где $C_2$ - другая произвольная константа.

Теперь сложим оба интеграла:

$F(x) = 2^x + C_1 + 3x + C_2$

Это и есть искомая первообразная функции $f(x)$ .

Теперь перейдем ко второй части вопроса - касательной прямой к графику функции $f(x)$ с уравнением $y=5x-2$ .

Касательная прямая имеет общую точку с графиком функции $f(x)$ , поэтому координаты этой точки должны удовлетворять обоим уравнениям. Для удобства, заменим $F(x)$ на $y$ , а $x$ на $a$ (координаты общей точки):

$y=5a-2$
$y=2^a+3a$

Теперь приравняем оба уравнения и найдем значение $a$ :

$5a-2=2^a+3a$

Перепишем уравнение в виде:

$2^a+5a-3a-2=0$

$2^a+2a-2=0$

Поскольку аналитическое решение этого уравнения в общем виде сложно найти, будем использовать численные методы (например, метод половинного деления или метод Ньютона), чтобы найти значение $a$ .

Таким образом, мы находим первообразную функции $f(x)$ и находим значение $a$ путем решения уравнения.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра