Для функции f(x)=3x^2-2 найдите первообразную, график которой проходит через точку м(2; 4) заранее за решение

F(x)=x^3-2x+c

y=x^3-2x+c

4=8-4+c

c=0

ответ:F(x)=x^3-2x

Для функции f(x)=3x² - 2 найдите первообразную, график которой проходит через точку М(2;4)

f(x) = 3x² - 2

F(x) = x³ - 2x + C

4 = 2³ - 2 * 2 + С

4 = 8 - 4 + C

4 + C = 4

C = 0

При первообразной заданной функции со значением константы равном нулю "0" ее график проходит через точку М(2;4)

F(x) = x³ - 2x + 0

F(x) = x³ - 2x (График первообразной оставлю в приложении).

Все первообразные функции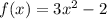 задаются формулой ( 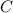- константа, которую нам хотелось бы найти):

По условию, нам сказано, что (первообразная) функция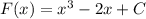 проходит через точку 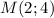. Это означает, что при подстановке 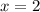получится :

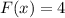Получаем, что константа равна нолю. Значит, искомая первообразная - это .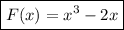

Задача решена! Функция вместе с ее первообразной также нашли себе место в приложении к этому ответу.