ДАЮ МАКСИМУМ! Для каждого значения параметра a определить число решений уравнения: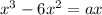
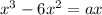
Другие вопросы по теме Алгебра
Популярные вопросы
- Построить б64 от (ля бемоль) построить м6 от (до диез)...
2 - 100 ! как можно назвать явление (проявление) геммитогенных перевауваций...
2 - Лучшая подруга учиться на 2, могут оставить на второй год и мы не...
2 - Как вы считаете были ли весной 1918г.какие-либо ильтернативы бретскому...
2 - Надо вставить запятые и разборы под цифрой 3,4 (3-морфологический...
3 - Перечислите основные последствия великих открытий: политические, ,...
2 - Укр у коробці є 5 однакових виробів, причому 3 з них пофарбовані....
3 - Укр на кульку нанесена сітка ічних координат. кулька кинута на площину....
3 - Обезьянам бананы. общий вес посылки составляет 40 кг. когда съели...
2 - (1)лиза не убежала с девчонками на реку. (2)все они стояли здесь,...
3
Перенесем все влево и вынесем за скобки :
:
Из этого следует, что уравнение всегда имеет хотя бы одно решение - . Задача сводится к тому, чтобы посмотреть, при каких
. Задача сводится к тому, чтобы посмотреть, при каких  будут корни у уравнения
будут корни у уравнения 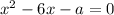 и сколько их будет. Для этого достаточно рассмотреть 2 ситуации.
и сколько их будет. Для этого достаточно рассмотреть 2 ситуации.
1) проверим, при каком значении корнем уравнения
корнем уравнения 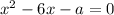 будет
будет  . Подставляем ноль в уравнение:
. Подставляем ноль в уравнение: 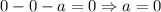 . При
. При 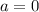 имеем:
имеем:
Делаем вывод, что при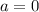 уравнение имеет два корня:
уравнение имеет два корня: 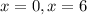 .
.
2) при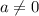 уравнение
уравнение 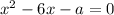 не может иметь корень
не может иметь корень  . Уравнение - квадратное. Сразу ищем дискриминант:
. Уравнение - квадратное. Сразу ищем дискриминант: 
Здесь рассматриваем 3 случая:
2.1. Если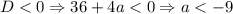 , то уравнение
, то уравнение 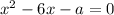 решений не имеет - следовательно, вторая скобка не будет давать новых решений и у исходного уравнения оно будет единственным.
решений не имеет - следовательно, вторая скобка не будет давать новых решений и у исходного уравнения оно будет единственным.
2.2. Если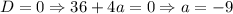 , то подставляя вместо параметра -9 в итоге получаем:
, то подставляя вместо параметра -9 в итоге получаем: 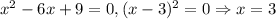 . Итого "вылез" еще один корень - значит, у исходного уравнения их будет два.
. Итого "вылез" еще один корень - значит, у исходного уравнения их будет два.
2.3. Если , то уравнение
, то уравнение 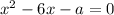 имеет два решения - следовательно, исходное будет иметь уже 3 решения. Заметим, что в это неравенство входит
имеет два решения - следовательно, исходное будет иметь уже 3 решения. Заметим, что в это неравенство входит 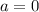 , а мы его проверяли отдельно - при
, а мы его проверяли отдельно - при 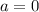 корней будет 2, а не 3, поэтому из неравенства его нужно исключить.
корней будет 2, а не 3, поэтому из неравенства его нужно исключить.
ОТВЕТ: При уравнение имеет единственный корень; при
уравнение имеет единственный корень; при 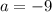 и
и 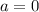 уравнение имеет два различных корня; при
уравнение имеет два различных корня; при 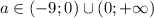 уравнение имеет три различных корня.
уравнение имеет три различных корня.