Даня задумал натуральное число, которое делится на 10, и имеет ровно 10 натуральных делителей. Какое число мог задумать Даня? Укажите

Question

Алгебра: Даня задумал натуральное число, которое делится на 10, и имеет ровно 10 натуральных делителей. Какое число мог задумать Даня? Укажите все возможные варианты.

tokmachevasvp01bjy · Answer

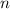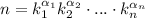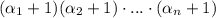В каноническом разложении числа на простые множители $n=k_1^{\alpha _1}k_2^{\alpha _2} \cdot ... \cdot k_n^{\alpha_n$ количество натуральных делителей по комбинаторному правилу умножения равно $(\alpha_1+1)(\alpha_2+1) \cdot ... \cdot (\alpha_n+1)$ .

Если число делится на 10, то начало разложения выглядит так:

$n=2^1 \cdot 5^1 \cdot ...$

Чтобы у числа было 10 делителей, произведение в вышеприведённой формуле должно быть равно 10. Число 10 раскладывается единственным образом на натуральные множители — к тому же простые: 2 и 5. Поэтому степень одного числа должна быть равна 5–1=4, а второго числа 2–1=1. Таких вариантов два:

$n=2^{2-1} \cdot 5^{5-1}=2 \cdot 5^4=1250\\n=2^{5-1} \cdot 5^{2-1}=2^4 \cdot 5=16 \cdot 5=80$