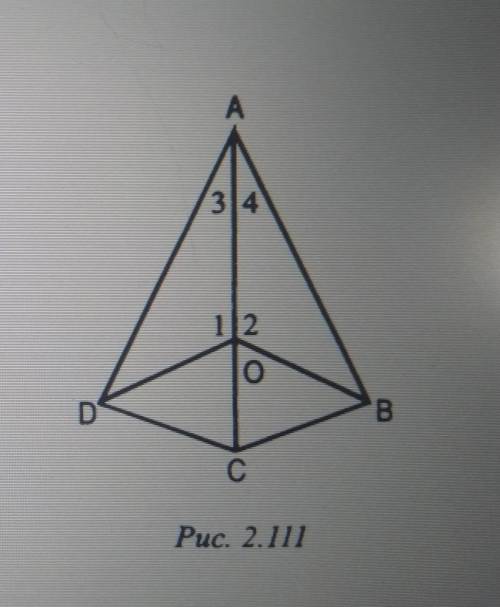
Дано: угол 1 = углу 2, угол 3 = углу 4.
Доказать: ∆ АВС = ∆ ADS​

Для доказательства равенства треугольников ∆АВС и ∆ADS, нам необходимо использовать некоторые свойства и определения геометрии.

1. Из технического задания известно, что угол 1 равен углу 2, а также угол 3 равен углу 4. Это дает нам две пары равных углов.

2. По определению углов, мы можем сказать, что углы 1 и 2 являются вертикальными, так как они находятся по разные стороны от пересекающей прямой AB. Аналогично, углы 3 и 4 также являются вертикальными.

3. Свойство вертикальных углов говорит нам, что вертикальные углы равны друг другу. То есть, угол 1 равен углу 2, и угол 3 равен углу 4.

4. Мы уже знаем, что углы 1 и 2 равны, а также углы 3 и 4 равны. Теперь нам нужно доказать, что стороны треугольника ∆АВС равны соответствующим сторонам треугольника ∆ADS.

5. Мы можем заметить, что сторона AB общая для обоих треугольников, так как это грань. Также, у нас есть равные углы 1 и 2, значит, мы можем применить свойство углов, а именно, углы при равных сторонах равны.

6. Следовательно, сторона AD также равна стороне AB, так как они являются прилежащими к равным углам. Мы доказали, что сторона AB равна стороне AD.

7. Подобным образом, мы можем доказать, что сторона AC равна стороне AS, так как углы 3 и 4 равны. То есть, сторона AC равна стороне AS.

8. Таким образом, мы доказали, что стороны треугольника ∆АВС равны соответствующим сторонам треугольника ∆ADS (AB = AD и AC = AS) и углы ∆АВС равны углам ∆ADS (углы 1 и 2, углы 3 и 4 равны).

9. По определению равных треугольников, если у них равны соответствующие стороны и углы, то треугольники сами равны. То есть, ∆АВС = ∆ADS.

Таким образом, мы доказали, что треугольник ∆АВС равен треугольнику ∆ADS, исходя из данных условия и основных свойств геометрии.