Дано квадратное уравнение 3x^2 + 2x + 1 - a = 0. найти все значения параметра а, при которых уравнение: а) не имеет корней б) имеет два равных корня в) имеет два различных корня г) не имеет корней на промежутке (-2; 1) д) имеет два
различных корня на промежутке (-2; 1) е) имеет хотя бы один корень на промежутке (-2; 1) ж) имеет ровно один корень на промежутке (-2; 1) з) не имеет корней, больших 1
Другие вопросы по теме Алгебра
Популярные вопросы
- Много ! напишите электронную схему атома азота и электронную формулу молекулы...
1 - Решите уровнения1) серная кислота + оксид алюминия - сульфат al + вода 2) гидроксид...
3 - Реши в) на хлебозаводе испекли за день в 5 раз больше мушек, чем пряников. сколько...
3 - Напиши вопросы к автору волшебник изумрудного города к 5 части 3 класс...
1 - Доклад о среднем веке 4 класс ! , !...
2 - Возьмем прямоугольный листок бумаги, который можно накрыть кругом. перегнем листок....
1 - Выпишите словосочетания прилагательное + существительное. рядом с каждым качественным...
1 - Чем знаменито озеро байкал? коротко...
2 - За время 5с тело массой 1300г (1,3 кг) двигаясь равноускоренно путь 70м. найти...
1 - Разложите на множители: (m+6)2 в квадрате - (n+2)2 в квадрате...
1
а) уравнение не имеет корней, когда D<0.
D=4-12(1-a)=12a-8<0
a<2/3
б) уравнение имеет 2 равных корня, когда D=0
12a-8=0
a=2/3
в) уравнение имеет 2 различных корня, когда D>0
12a-8>0
a>2/3
г) данный случай включает в себя значения а из пункта а)
и рассмотрим случай, когда D>0 и a>2/3
Тогда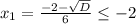 и
и 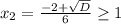 . Из первого неравенства следует, что
. Из первого неравенства следует, что 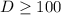 , из второго
, из второго 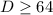 . Следовательно,
. Следовательно, 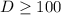 .
.
12a-8>100
a>9
д) Значит D>0. И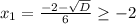 и
и 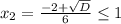 . Тогда
. Тогда 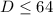 .
.
е) Значит .
.
ж)
з)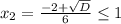 . Тогда
. Тогда 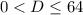 .
.