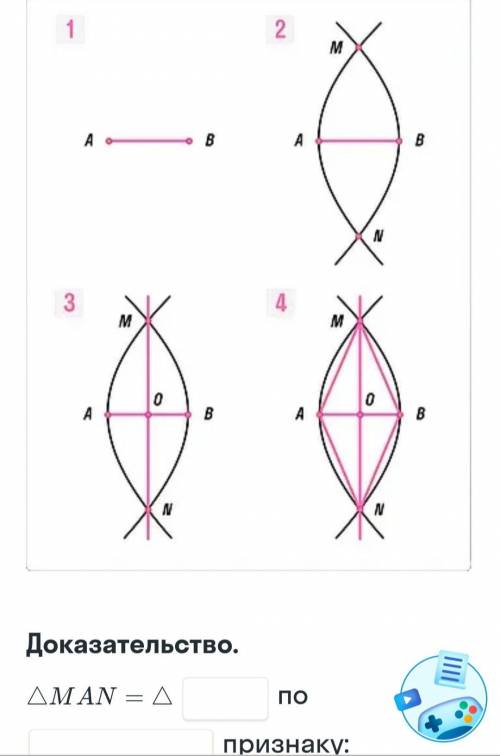
Дано:AB-отрезок

Построить:прямую

MN AB:AB MN=O, AO=OB

Для построения прямой MN, пропорциональной отрезку AB, с отношением AB:MN=O, где O- некоторое число, и при условии, что AO=OB, мы можем использовать следующий метод:

1. Возьмем компас и опишем окружность с центром в точке O и радиусом, равным AB.

2. Проведем две хорды через точки A и B в любом удобном направлении. Для примера, проведем прямую через точки A и B, перпендикулярную отрезку AB.

3. Пересечение этой прямой и окружности в точках M и N будет задавать отрезок MN, пропорциональный отрезку AB.

Обоснование:

Окружность, проходящая через точки A и B с радиусом AB, будет нужна нам для того, чтобы построить прямую, пропорциональную данному отрезку. Концы отрезка AB нам дадут две точки для проведения хорды. Исходя из условия задачи, что AB:MN=O, AO=OB, мы можем сделать вывод, что М и N лежат на радиусе окружности, равном O*AB. При этом, поскольку радиус окружности является прямой линией, все точки на ней будут пропорциональны отношению AB:MN.

Шаги решения:

1. Возьмите циркуль и поставьте его концы на точки A и B. Опишите окружность с центром в точке O с радиусом AB.

2. Возьмите линейку или прямой циркуль и проведите прямую через точки A и B, перпендикулярно отрезку AB. Обозначим пересечение этой прямой с окружностью как точки M и N.

3. Теперь имеется прямая MN, которая будет пропорциональна отрезку AB с отношением AB:MN=O.

Итак, с помощью этого метода мы можем построить прямую MN, которая будет пропорциональна отрезку AB с заданным отношением и условием AO=OB.