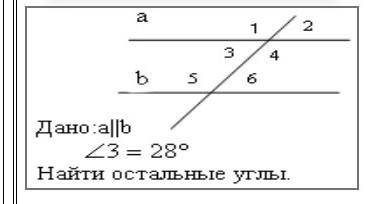
Дано:а||b угол 3=28° найти остальные углы​

Обозначим углы данного треугольника как угол 1, угол 2 и угол 3.

Так как линии а и b || (параллельны), то по свойству соответственных углов угол 1 и 3 будут равными. Значит, угол 1 = угол 3 = 28°.

Также, угол 3 и угол 2 составляют при сопряжении линий а и b внутренние прилежащие углы, и по свойству второстепенных углов они будут суммироваться в 180°. Значит, угол 3 + угол 2 = 180°.

Заменим угол 3 на 28° в последнем уравнении:
28° + угол 2 = 180°.

Теперь, чтобы найти угол 2, вычтем 28° из обеих частей уравнения:
угол 2 = 180° - 28° = 152°.

Таким образом, мы нашли два угла треугольника: угол 1 = угол 3 = 28° и угол 2 = 152°.

Остается угол 1, который мы можем найти, применив свойство суммы углов треугольника, которое гласит, что сумма всех углов треугольника равна 180°:
угол 1 + угол 2 + угол 3 = 180°.

Подставим значения углов 1 и 2:
28° + 152° + угол 1 = 180°.

Вычтем 28° + 152° из обеих частей уравнения:
угол 1 = 180° - (28° + 152°) = 180° - 180° = 0°.

Таким образом, все углы треугольника найдены: угол 1 = 0°, угол 2 = 152° и угол 3 = 28°.