Дана прямая l1. прямая l2 проходит через точку m параллельно прямой l1. найдите указанные коэффициенты: l1: 3x-2y-10=0, м(2; -1), l2: ax+by-8=0
а=?
b=?
Другие вопросы по теме Алгебра
Популярные вопросы
- Упростите выражение и найдите его значение 18а-12а+3с-2с при а=5 с=21...
3 - Қосылыстардағы химиялық байланыс түрлері олардың ерітінділері мен балқымаларының...
2 - Прочтите текст и заполните пропуски в предложениях. Завершающим этапом...
3 - Заполните таблицу Буквы ё о е и после шипящих и ц в корнях и окончаниях...
3 - Шо вивчають в кабінеті біології...
1 - два кути одного трикутника дорівнюють двом кутам другого трикутнику Знайдіть...
3 - Для класу привезли 13 підручників з англійської мови, 8 словників та...
1 - при якому значенни х значення виразив 4х+5, 7х-1, х\2+2 будуть послидовними...
1 - Коли з явилися перші писемні згадки про територію України? Ком вони належать?...
3 - Мануфактура дегеніміз не?...
1
Поскольку точка М принадлежит прямой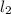 , то подставляя координаты точки М, мы получим
, то подставляя координаты точки М, мы получим
Прямые параллельны, если их угловые коэффициенты равны, т.е.
Тогда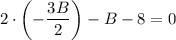 или
или 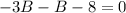 откуда
откуда 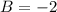 , тогда
, тогда 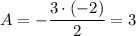
ответ: А = 3; B = -2.