1. Алгебра
  2. Дана функция y = - 8x

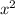Дана функция y = x^{2} - 8x + 7 a) запишите координаты вершины параболы;

b) определите, в каких четвертях находится график функции;

c) запишите ось симметрии параболы;

d) найдите точки пересечения графика с осями координат;

e) постройте график функции

umnik250 umnik250    1   01.03.2021 07:14    2

Ответы
380973599293 380973599293  31.03.2021 07:14

1)\ \ y=x^2-8x+7\\\\a)\ \ x_{v}=-\dfrac{b}{2a}=-\dfrac{-8}{2}=4\ \ ,\ \ y_{v}=y(4)=16-32+7=-9\\\\Vershina\ \ V(\, 4\, ;\, -9\, )\\\\c)\ \ os\flat\ simmetrii:\ \ x=4\\\\d)\ \ OX:\ x^2-8x+7=0\ \ ,\ \ x_1=1\ ,\ x_2=7\ \ (teorema\ Vieta)\\\\A(1;0\, )\ ,\ \ B(7;0\, )\\\\OY:\ \ x=0\ \ \to \ \ y(0)=7\ \ ,\ \ \ C(\, 0;7\, )

e)  См. рис.

b)  график находится в 1,2 и 4 четвертях .  


Дана функция y = - 8x + 7 a) запишите координаты вершины параболы; b) определите, в каких четвертях
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Alena26vl Alena26vl  17.03.2021 19:23
алгебра 9 классРозв язати рівняння ​...
hades77 hades77  17.03.2021 19:22
график а) функции Y = x ^ 2-2x-3, наклонить ось, обосновать ответ б) Найдите точки пересечения графика с осью Ox в) Найдите ось симметрии г) Нарисуйте график...
irinamiller93 irinamiller93  17.03.2021 19:22
Можете решить все нечетные, наприме под цифрой 1; 3; 5 и т.д​...
curlyprettygirl curlyprettygirl  17.03.2021 19:22
3. Функция задана уравнением . a) В какой точке график данной функции пересекает ось ОY?b) Найдите точки пересечения графика функции с осью ОХ.c) Запишите уравнение оси симметрии...
Sofia1111111111811 Sofia1111111111811  17.03.2021 19:22
мне надо сделать да завтра.​...
Klinyushina Klinyushina  20.04.2021 22:50
Сколькими можно взвесить на рычажных весах 20кг риса, используя гири 1кг, 2кг, 5кг?​...
feeedf feeedf  20.04.2021 22:50
1204. За перший день 2 гусеничних трактори й один колісний 30- рали 22 га, а за другий день 3 гусеничних і 8 колісних - 72 га.Знайдіть, скільки гектарів землі може зорювати...
25marta52 25marta52  20.04.2021 22:49
Розвязати додавання систему рівнянь {8х+3у=1 {2х-4у=-18...
yanarem1 yanarem1  20.04.2021 22:49
На столе лежит пять кучек монет количество монет во всех пучках попарно различные разрешается выбрать самую маленькую кучку монет и добавить в неё четыре монеты затем проделать...
Pharmit24 Pharmit24  18.09.2019 22:10
Найдите сумму наибольшего и наименьшего целых решений неравенства -448.9 2.9 + 9x 23.6...

Популярные вопросы