1. Алгебра
  2. Дана функция у=-(3х-1)^5/3+20х

Дана функция у=-(3х-1)^5/3+20х 1). исследуйте функцию на монотонность и экстремумы; 2). найдите наибольшее и наименьшее значения функции на полуинтервале (1; 3].

Riyaa Riyaa    3   12.06.2019 18:20    4

Ответы
nemcevakata401 nemcevakata401  10.07.2020 06:51

y=\frac{-(3x-1)^5}{3+20x}

1. Область определения функции: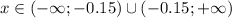 x \in (-\infty;-0.15)\cup (-0.15;+\infty)

2. Первая производная

y'=- \dfrac{15(3x-1)^4(3+20x)-(3x-1)^5\cdot20}{(3+20x)^2}=\\=- \dfrac{(3x-1)^4(45+300x-60x+20)}{(3+20x)^2}=- \dfrac{(3x-1)^4(240x+65)}{(3+20x)^2}

3. Точка пересечения с осью Ох

-(3x-1)^5=0 \\ x= \frac{1}{3}

(1/3;0) - - точка пересечения с осью Ох

4. Точки пересечения с осью Оу.

x=0 \\ y(0)= \frac{-(3\cdot0-1)^5}{3+20\cdot0} = \frac{1}{3}

(0;1/3) - точкa пересечения с осью Оу

5. Критические точки

y'=0 \\ (240x+65)(3x-1)^4=0 \\ x_1=- \frac{13}{48} \\ x_2= \frac{1}{3}

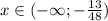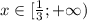
Функция возрастает на промежутке x \in(-\infty;- \frac{13}{48} ), а убывает - x\in(- \frac{13}{48} ;-0.15),~ x\in (-0.15; \frac{1}{3} ] и x \in [\frac{1}{3} ;+\infty)

В т. х = -13/48 - функция имеет локальный максимум,

Теперь дан нам отрезок.


y(3)=- \frac{(3\cdot3-1)^5}{3+20\cdot3} =- \frac{32768}{63}=-520


\displaystyle \max_{(1;3]}\,\,y(x)= \lim_{x \to1^+} y(x)=- \frac{32}{23}

\min_{(1;3]}\,\,y(x)=y(3)=-520


Дана функция у=-(3х-1)^5/3+20х 1). исследуйте функцию на монотонность и экстремумы; 2). найдите наиб
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Васька11114322 Васька11114322  08.07.2019 08:00
Найдите значение выражения квадратный корень из 9b^2 - корень 3 степени из 8b^3 - корень 4 степени из 256b^4 + корень 8 степени из 2401 при b= (корень из 7) -3...
Нура191 Нура191  08.07.2019 08:00
Представьте в виде произведения: a*a*a-3ab-2a*a*b+ 6b*b...
SanyaLuckYouTube SanyaLuckYouTube  08.07.2019 08:00
Найдите корни уравнения x-9/x-2+x+5/x+2=2...
546546YGygY 546546YGygY  08.07.2019 08:00
Вычислить пределы функций lim x^3+4x^2+5x+2/x^3-3x-2 x- -1...
Nejdan1 Nejdan1  16.03.2020 21:54
Определите, какие из данных чисел не являются решением системы неравенствВАРИАНТЫ ОТВЕТА :232,513,5​...
Alinok99 Alinok99  16.03.2020 21:54
квадратные уравнения 5 не надо...
alah200 alah200  16.03.2020 21:54
Не решая уравнение, найти суму и произведение его коней: 5x²-3x-18=0...
Inpeakfhdh Inpeakfhdh  16.03.2020 21:54
В квадратных скобках Номера 1; 2; 3 очень...
sinocek1 sinocek1  16.03.2020 21:54
2cos(x/2+П/6)-✓3=0 Розв яжіть будь ласка...
minchuna2016p02voj minchuna2016p02voj  16.03.2020 21:54
Разложите на множители:36s^2-12su+u^2​...

Популярные вопросы