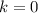Дана функция  при каких значения k прямая y=kx не имеет с графиком ни одной общей точки
при каких значения k прямая y=kx не имеет с графиком ни одной общей точки
Другие вопросы по теме Алгебра
Популярные вопросы
- Прочитайте слова. З ясуйте, чи вони споріднені. Три, третій, триколісний,...
3 - девочки пишите в ком номера есть группа для к-поперов название группы *Бродячие...
3 - Расставьте знаки препинания. Подчеркните однородные члены предложения. Яркое...
1 - Учні третього класу зібрали 300 кг макулатури за 6 днів, а четрвертого -...
1 - сторона основи правильної чотирикутної піраміди 6√2 а бічне ребро кут 45°...
1 - Геометрія. Правильні многокутники...
2 - куркиретеды, табигаттын, армандады, женылдегу, енбек куралдарын, касыпке,...
2 - Читайте знаменитые строки из экранизаций в картинках. Сопоставьте их сперсонажи...
3 - Хто швидше почує голос співака: глядач у залі, що сидить на відстані 10,2...
1 - 1. Поясніть, чому Україна входить до складу країн-лідерів із виробни- цтва...
1
Тут рационально написать так: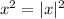
Напишем ОДЗ функции:
Упростим функцию:
Нарисуем график этой функции (на месте ОДЗ точки выколоты). (Рисунок строем таблицей; рисунок схематический.)
Функция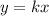 — это прямая, проходящая через начало координат. С данным графиком она не будет имеет общих точек в 3 случаях:
— это прямая, проходящая через начало координат. С данным графиком она не будет имеет общих точек в 3 случаях:
случаи, когда проходит через выколотые точки (их две);когда коэффициентЕсли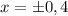 , то
, то 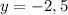 . Отсюда:
. Отсюда: 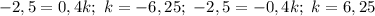
ответ: прямая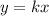 не будет иметь с графиком функции
не будет иметь с графиком функции 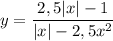 не одной общей точки при
не одной общей точки при 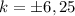 и
и