Дан треугольник ABC BK=8cm, и AM=6cm - высоты треугольника, AC = 15cm. Найдите Длину стороны BC
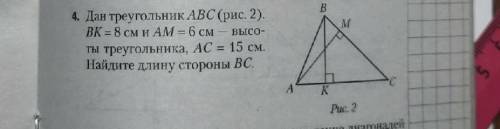
Другие вопросы по теме Алгебра
Популярные вопросы
- Что стало с после нидерландской революции?...
3 - Иэ двух городов расстояние. между которыми 484 км выехали одновременно навстречу...
1 - Уматери первая группа крови, а у отца четвертая. могут ли дети унаследовать...
2 - Вмагазин завезли 800кг яблок,причём 50% в магазин завезли 800кг яблок,причём...
3 - Решить эти примеры 3912: 12 6748: 14 10635: 15 11206: 13 14562: 18 15640:...
3 - Решите уравнения: 1) |x|=5; 2) |7x|=56; 3) 3|x|=123; 4) -|x|=-71 5)|-x|=-4;...
3 - Первое упоминание о городе москве относился к 1147 году.в каком году москве...
3 - Вкаком веке была куликовская битва обазначте век и год...
3 - Решите уравнения 7х - 3.2 - 2х + 1 7 - 2а при а=-0.5...
3 - Какие превращения энергии имеют место в электрическим звонке во время работы...
2
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к противоположной стороне. В данной задаче, AM и BK - высоты треугольника, поэтому они перпендикулярны боковым сторонам треугольника.
Теперь, когда мы знаем, что такое высота треугольника, перейдем к решению задачи.
Мы знаем, что AM = 6 см, и в данной задаче мы хотим найти длину стороны BC. Для этого нам понадобится использовать свойство этих высот, а именно то, что они делят основание треугольника на две равные части.
Для начала, мы обозначим точку пересечения высот AM и BK как точку H. Тогда, точка H будет являться медианой треугольника ABC (точкой, делящей сторону на две равные части).
Таким образом, мы можем сделать вывод, что BH = KH, так как они являются радиусами равных окружностей.
Далее, мы можем обозначить точку пересечения медианы AH и BC как точку M. Тогда, точка M будет являться центром окружности, вписанной в треугольник ABC.
С использованием этой информации, мы можем применить свойство радикальной оси. Согласно этому свойству, если существуют три окружности, их радикальные оси пересекаются в одной точке.
В данной задаче, мы имеем три окружности:
1) Окружность с центром в точке B и радиусом BK.
2) Окружность с центром в точке A и радиусом AM.
3) Окружность, вписанная в треугольник ABC.
Следовательно, радикальная ось этих трех окружностей проходит через точку M.
Теперь, используя полученные знания, мы можем найти длину стороны BC. Для этого, нам понадобится представить решение в виде пошагового алгоритма:
Шаг 1: С использованием формулы площади треугольника, найдем его площадь. Площадь треугольника ABC можно вычислить по формуле:
Площадь ABC = (1/2) * AC * AM
Подставляем значения:
Площадь ABC = (1/2) * 15 * 6 = 45 кв. см
Шаг 2: С использованием формулы площади треугольника, найдем площадь треугольника ABH. Площадь треугольника ABH можно вычислить по формуле:
Площадь ABH = (1/2) * BH * AH
Подставляем значения:
Площадь ABH = (1/2) * BH * 15 = 45 кв. см
Шаг 3: С использованием формулы площади треугольника, найдем площадь треугольника CBH. Площадь треугольника CBH можно вычислить по формуле:
Площадь CBH = (1/2) * BH * CH
Так как CH = AC - AH, подставляем значения:
Площадь CBH = (1/2) * BH * (AC - AH) = (1/2) * BH * (15 - 15) = 0 кв. см
Шаг 4: Сумма площадей треугольников ABH и CBH должна быть равна площади треугольника ABC. То есть,
Площадь ABH + Площадь CBH = Площадь ABC
Подставляем значения:
45 + 0 = 45
Таким образом, получаем уравнение:
45 + 0 = 45
Это уравнение с одной неизвестной - длиной стороны BC. Путем решения этого уравнения мы сможем найти длину стороны BC.
Однако, если обратить внимание на пункт "Шаг 3", мы видим, что площадь треугольника CBH равна 0 кв. см. Значит, треугольник CBH является вырожденным (одна его сторона равна 0). Следовательно, сторона BC также должна быть равной 0 см.
Таким образом, длина стороны BC равна 0 см.