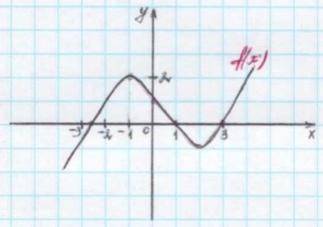
Дан график функции f(x): (фото ниже)
f'(x) > 0 на промежутках..........
f'(x) < 0 на промежутках.........
точки максимума функции f(x).........
точки минимума функции f(x) ......

f'(x) > 0 на (-∞; -1) и на (2; +∞)

f'(x) < 0 на (-1; 2)

точка максимума х = -1

точка минимума х = 2

производная там будет больше нуля, где функция возрастает, а именно на промежутках [-3.9;-1] и [2;4.2] и соответственно  производная меньше нуля, если функция убывает. здесь по графику видно, что х∈[-1;2]

Точки экстремума - это точки, при переходе через которые которых функция меняет характер, а производная знак.

Точка максимума - х=-1, в ней возрастание сменяется на убывание, и производная меняет знак с плюса на минус, и х=2- точка минимума, т.к. при переходе через нее производная меняет знак с минуса на плюс, а функция характер с убывания на возрастание.