Cos2x+sin^2x=0,25 + отобрать корни на отрезке [3pi; 9pi/2]
Другие вопросы по теме Алгебра
Популярные вопросы
- Периметр равнобедренного треугольника равен 32,а основание 12.найдите площадь...
2 - Надо узнать падеж. след собачий ведет к конуре. к конуре какой падеж?...
2 - По горизонтальной дороге движутся в одном направлении грузовик массой 5т со скоростью...
1 - Почему в ночь на ивана купала цветёт папоротник?...
1 - Молочный завод отправил в магаз 56 ящиков масла, по 20 кг в каждом. за день продали...
1 - Как ты думаешь, почему юго-западная русь избрала союз с католической европой против...
2 - Вычисли сумму одинаковых слагаемых 5+5+5+5 и 3+3+3...
3 - Решите пример, (4488: 264+12605)×57-63209= по действиям...
3 - Почему трудно пить сырое яйцо, если в нем есть толь¬ко одно отверстие? какую роль...
1 - Почему учителю не понравилось окончание текста у сережи? зайчик ел морковку,а...
1
Отбор корней на отрезке:
нет таких
ответ:
Распишем cos2x как 1-2sin²x
1-2sin²x+sin²x=0,25
-sin²x=-0,75
sin²x=0,75
sin²x=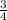
sinx=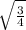
sinx=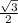
sinx=a
x=(-1) arcsina+πn n принадлежит z
arcsina+πn n принадлежит z
x=(-1) ·
·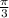 +πn n принадлежит z
+πn n принадлежит z
sinx=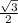
x=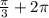 n n принадлежит z
n n принадлежит z
x=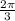 +2πn n принадлежит z
+2πn n принадлежит z
К твоему отрезку принадлежит только первый корень
x=(-1) ·
·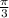 +πn n принадлежит z
+πn n принадлежит z