Cos 5x cos 7x -sin 5x sin 7x = -√3/2
решите уравнение
Другие вопросы по теме Алгебра
Популярные вопросы
- Населення Індії поділялося на групи ???...
3 - Представьте выражение в виде многочлена. (a в квадрате− 3a) в квадрате...
1 - Как вы думаете если качества хитреца использивать и вспомнить то...
1 - 1) Перехід армії Цезаря через яку річку ознаменував початок громадянської...
2 - Люди СРОЧЬНО Люди срочьно.до розчину мосою натрій хлориду масою 100г...
3 - Напишите рассказ 100-120 слов от имени путешественника посетившего...
2 - Продолжи фразу:Основными стадиями движения продукта являются: производство,...
1 - Задание по сольфеджио построить 2 и 3 задание Очень...
1 - Яку масу сахарози необхідно додати до 200 г води, щоб виготовити...
1 - с задачей геометрия 7 класс Найдите угол AQB между биссектрисами...
3
Для начала нам нужно упростить левую часть. Воспользуемся формулой косинуса суммы: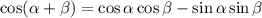 , применим её для нашего уравнения.
, применим её для нашего уравнения.