Cколько целых корней имеет уравнение: |x-1|*|x+2|=4?
Løæålø
3
27.09.2019 18:30
0 
Популярные вопросы
- Визначте валентність і стурінь окиснення всіх елементів за наведеними структурними...
1 - ответить на вопрос. Акакий Акакиевич Башмачкин - посмешище или несчастный.Дайте...
1 - Особливості розвитку держави Русі-України в період становлення (IX - перша...
1 - Составьте структурные формулы алкенов, по их названиям....
1 - Мюзикл «Ромео и Джульетта» Продумайте и запишите ключевые слова, которыми...
1 - Выделите грамматическую основу в каждом предложении. Укажите вид сказуемого....
3 - 400000+360016:4. Результат первого действия равен .Результат второго действия...
2 - Как называются короткие звуки музыка б...
2 - В бессемеровском получения стали окислителями являются..восстановителями?...
3 - 166. Раскройте скобки и вставьте пропущенные буквы. Подчеркните деепричастия....
2
Умножим
на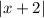 
:
Разделим каждый член на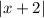
и упростим.
Перепишем уравнение с абсолютным значением без знака модуля:
После упрощения остаются только два уникальных уравнения, которые нам предстоит решить:
Решим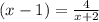
относительно x:
Решим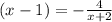
относительно x:
Запишем все решения:
(х-1)*(х+2)=4
(х+1)*(х+2)=-4
х=2
х=-3
х=-3,х=2