1. Алгебра
  2. Цифры некоторого натурального

Цифры некоторого натурального числа идут в порядке возрастания. Может ли оно делиться на 11?

Qweyudbdbf Qweyudbdbf    2   20.06.2021 12:33    2

Ответы
Жека331211 Жека331211  20.07.2021 13:13

ответ: делиться на 11 такое число не может.

Обоснование. Как известно, число делится на 11 тогда и только тогда, когда сумма цифр, стоящих на нечетных местах, отличается от суммы цифр, стоящих на четных, на число, делящееся на 11 (как частный случай эти суммы могут совпадать). Однако в нашем случае максимальное возможное отличие равно 8 (из двузначных это число 19, из трехзначных 129, 239, ..., 789).  Докажем, что больше 8 никогда не получится.

1) Пусть в числе четное число знаков: a_1a_2\ldots a_{2n}. Тогда

(a_{2n}-a_{2n-1})+\ldots +(a_2-a_1) - это часть расстояния от  a_1 до a_{2n}, а поскольку первая цифра не меньше 1, а последняя не больше 9, эта сумма не больше 8.

2) Пусть в числе нечетное число знаков: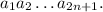 a_1a_2\ldots a_{2n+1}. Тогда

a_{2n+1}-a_{2n}+\ldots -a_2+a_1=a_{2n+1}-((a_{2n}-a_{2n-1})+\ldots +(a_2-a_1)),

то есть из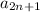 a_{2n+1} вычитается часть расстояния между a_1 и a_{2n}

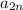
Поэтому снова больше 8 получиться не может.

Но одновременно мы видим, что  0 также не может получиться.

Вывод: число, у которого цифры идут в порядке возрастания, на 11 делиться не может.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Saca2000 Saca2000  17.12.2020 01:44
Найдите область определения функции,используя метод интервалов:y=√x-4√x +1​...
nicishcina nicishcina  17.12.2020 01:49
Вычислить i^1534 - i^97 + 2i^452 - 4i^1001...
Skelet001 Skelet001  17.12.2020 01:51
с алгеброй (логарифмы)3(log2x)^2+13log2x-10=0...
milankagl milankagl  17.12.2020 01:53
цена на хрустальную вазу а р. Из-за смены тарифов на энергоносители цена выросла на 45% ,а после увеличения арендной платы в магазине ещё на 20% . Какова цена люстры?​...
shhfxecbhawc shhfxecbhawc  17.12.2020 01:58
Пятнадцать икс квадрат плюс два икс минус один равно ноль...
NASTEN111 NASTEN111  17.12.2020 02:02
Выполните до завтра нужно! Заранее...
Аня3321 Аня3321  03.07.2019 04:30
10x квадрате+5x-5 . найти корни квадратного трехчлена...
mrtwice mrtwice  03.07.2019 04:30
Из двух городов, расстояние между которыми равно 540 км, навстречу друг другу одновременно выехали два автомобиля. найдите скорость второго автомобиля, если скорость первого...
artemkharlamov1 artemkharlamov1  03.07.2019 04:20
Вычислить: 65/7+16/9 / (12/5-4/3)*3/7...
amankeldievan amankeldievan  11.04.2021 11:03
Задача по Теории вероятностей Первое предприятие может получить банковский кредит с вероятностью 0,9, второе и третье - с вероятностями, что удовлетворяют системе уравнений:...

Популярные вопросы