Число 9 представьте в виде суммы двух неотрицательных слагаемых так, чтобы произведение квадрата одного из них на утроенное другое слагаемое было наибольшим.
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему опасны кожные заболевания...
2 - Описать этапы жизненного цикла на примере любой программы (эл учебник, тест...
1 - 11 Thinking: Read the story again and match.cap2 They can t cooka because...
1 - Выбери характеристику озона: 1.хороший растворитель2.в лаборатории получают...
2 - Андерсен назвал свое произведение Снежная королева сказкой из семи рассказов....
3 - Вглубь строки Задание 126• Объясните смысл афоризмов: Самая большая роскошь...
2 - Что такое синонимы антонимы Т главные члены предложение...
3 - . В числе 9043 206 отделите запятой одну цифру справа и прочи- тайте получившуюся...
3 - Шар массой 414 г сталкивается со вторым шаром неизвестной массы. Ускорения,...
3 - Эссе на тему What you need to do in order not get sick in winter .пишем...
3
Для того, чтобы найти наибольшее значение произведения квадрата одного из них на утроенное другое слагаемое, составим функцию: пусть первое число будет х, а второе (9-х). Тогда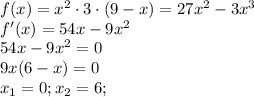
Первое число не подходит по условию задачи, следовательно искомое число равно 6, а второе 9-6=3.
ответ искомые числа 6 и 3: 9 = 6 + 3;