1. Алгебра
  2. Число 6 является корнем уравнения

Число 6 является корнем уравнения x^2 + bx - 30 = 0

Найдите значение b и второй корень уравнения.

Число -1/6 является корнем уравнения 3x^2+mx+2=0

Найдите значение m и второй корень уравнения.

SashaNemur SashaNemur    3   14.03.2020 22:30    28

Ответы
гол38 гол38  11.10.2020 21:38

Применяем теорему Виета.

1)\; \; x^2+bx-30=0\\\\x_1=6\; \; \to \; \; 6\cdot x_2=-30\; \; \to \; \; x_2=-5\\\\b=-(x_1+x_2)=-(6-5)=-1\\\\\\2)\; \; 3x^2+mx+2=0\\\\x_1=-\frac{1}{6}\; \; \to \; \; -\frac{1}{6}\cdot x_2=\frac{2}{3}\; \; ,\; \; x_2=-4\\\\m=-\frac{x_1+x_2}{3}=-(-\frac{1}{6}-4):3=\frac{25}{3}:3=\frac{25}{18}

ПОКАЗАТЬ ОТВЕТЫ
rafik321 rafik321  11.10.2020 21:38

Відповідь:

b=-1

x2=-5

2) b=16.5

x2=-2

Пояснення:

1) За теоремой Виета

x_{1}+x_{2} = \frac{-b}{a} \\x_{1} *x_{2} =\frac{c}{a}

подставим значения получим систему

\left \{ {{6} +x_{2} =-b} \atop {6*} x_{2} =-30}} \right.

x2=-30/6

x2=-5

6-5=-b

b=-1

2)\left \{ {{\frac{-1}{6} }+x_{2} =-\frac{b}{3} } \atop {\frac{-1}{6} *} x_{2} =\frac{2}{3} }} \right.

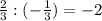
x2=\frac{2}{3} :(-\frac{1}{3}) =-2

-1+6*(-2)=-2b

b=16.5

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
alina28551 alina28551  01.03.2020 20:53
Найдите уравнение касательной к графику функции y=8x³-4x+3 в точке x0=2 Исследовать функцию и построить эскиз графика y=x³-2x²+3 Найдите наибольшее и наименьшее значение функции...
tahliaderma tahliaderma  01.03.2020 20:51
Дана геометрическая прогрессия (хn) знаменатель который равен -3 х 1=-6 Найдите х5...
Anastasia0610201 Anastasia0610201  01.03.2020 20:50
Преобразите многочлены 1) (2x+x^3)^22) (c^2-3a)(c^2+3a)​...
arekhvanova arekhvanova  01.03.2020 20:38
(2х2+3у3)(3у3-2х2) при х4=1/2 , у2=2​...
natali3171 natali3171  01.03.2020 20:35
Как преобразовать квадрат двучлена в многочлен стандартного вида. Пример (-3а + 5х)^2...
DC2004 DC2004  01.03.2020 20:34
с алгеброй 10 класс уравнения...
ВероникаКарпова ВероникаКарпова  01.03.2020 20:31
Доказать тождество:1)ctg2a-sin4a=cos4a*ctg2a2)1+cos(3pi+3a)cos2a-cos(1,5pi-3a)sin2a=2sin²2,5a3)tg⁴a(8cos²(pi-a)-cos(pi+4a)-1)=8sin⁴aЭто самый дурацкий номер в учебнике......
Maria2005y Maria2005y  18.11.2019 00:27
Преобразуйте выражение в многочлен стандартного вида 269 б...
Gamoo Gamoo  18.11.2019 00:22
Запишите нормально с решением и все буквы от а до е...
РукиКрабы111111111 РукиКрабы111111111  18.11.2019 00:20
С10 , не понял как его делать, если можно желательно с объяснением...

Популярные вопросы