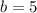Число -6 є коренем рівняння x2 + bx -6 =0. Знайдіть другий корінь рівняння і значення b
Другие вопросы по теме Алгебра
Популярные вопросы
- Найти частные производные первого порядка функций двух переменных...
3 - Какие реки протекают по территории Мирзачульского района...
1 - По какой причине схожи животный и растительный мир палеографический и неорганические...
2 - Сорта-труженники и сорта-рекордсмены (в чем отличие, когда появились)...
2 - 1. Какие чувства вызвало у вас чтение отрывка из романа? Что возмутило...
1 - родной язык уйгуров. во они одевались , традиции , на какой територии жили...
1 - Какое правило можно придумать к этому знаку...
3 - начертить корпус детали с размерами....
1 - Визначити і записати, які проблеми автор підіймає у творі Запах думки ...
3 - Расскажите о жизни римских горожан?...
2
х² + bx - 6 = 0
якщо х₁ = -6
(-6)² + b · (-6) - 6 = 0
36 - 6b - 6 = 0
30 - 6b = 0
-6b = -30
b = -30 : (-6)
b = 5
- - - - - - - - - -
х² + 5х - 6 = 0
D = b² - 4ac = 5² - 4 · 1 · (-6) = 25 + 24 = 49
√D = √49 = 7
х₁ = (-5-7)/(2·1) = (-12)/2 = -6
х₂ = (-5+7)/(2·1) = 2/2 = 1
Вiдповiдь: х₂ = 1; b = 5.
За теоремою Вієта другий корінь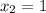 , тоді
, тоді 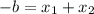 звідси
звідси