Четыре числа образуют геометрическую прогрессию. Если к ним прибавить соответственно 3, 12, 13 и 22, то получим четыре числа, образующие арифметическую прогрессию. Определи числа, образующие геометрическую прогрессию.
ответ:
знаменатель геометрической прогрессии: q=
.
Члены геометрической прогрессии:
b1=
b2=
b3=
b4=
Другие вопросы по теме Алгебра
Популярные вопросы
- Жизненные проблемы Петра в фильме слепой музыкант...
2 - сочинение по рассказу *в дурном обществе* на тему-почему Вася подружился...
3 - Розкладіть на множники першим х у квадраті відняти ігрик у квадраті...
2 - Yordam bervorilar 303mashq...
2 - 2. Сайлемдерді көшіріп жаз. 1. Қарлығаш төбеде қонақтап отыр. 2....
2 - В чем великодушие стариков в рассказе ма-аленькая?...
2 - Как быстро выучить текст по английскому за день или 3 часа ?) мне...
3 - 2 13. Если кран за 6 часов наполнитбассейна,5то за какое время он...
1 - найти монолог Тараса. Чтение 3 класс ефросинина...
3 - Подчеркнуть подлежащее и сказуемое. 1) Василий Андреевич Жуковский...
2
Пуcть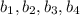 - члены геометрической прогрессии,
- члены геометрической прогрессии, 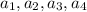 - члены арифметической прогрессии.
- члены арифметической прогрессии.
Использовав формулу общего члена прогрессии, перепишем члены геометрической прогрессии в следующем виде: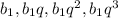 .
.
По свойству арифметической прогрессии, каждый ее член равен среднему арифметическому двух соседних с ним членов:
По условию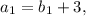
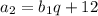 ,
, 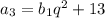 ,
, 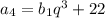 .
.
Итого:
Решаем систему:
Теперь мы можем вычислить члены геометрической прогрессии:
ОТВЕТ: 2; -2; 2; -2.