1. Алгебра
  2. Четыре числа, которые образуют

Четыре числа, которые образуют прогрессию, первый член которой меньше третьего на 24, а второй больше четвертого на 8

Катюша1233210 Катюша1233210    3   01.07.2019 01:30    1

Ответы
ната5810 ната5810  24.07.2020 13:53
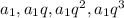a_1, a_1q, a_1q^2, a_1q^3 - искомые члены геометрической прогрессии.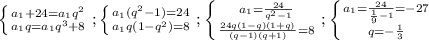
\left \{ {{a_1+24=a_1q^2} \atop {a_1q=a_1q^3+8}} \right. ; \left \{ {{a_1(q^2-1)=24} \atop {a_1q(1-q^2)=8}} \right. ; \left \{ {{a_1= \frac{24}{q^2-1} } \atop { \frac{24q(1-q)(1+q)}{(q-1)(q+1)}=8 }} \right.; \left \{ {{a_1= \frac{24}{ \frac{1}{9}-1}=-27 } \atop {q=- \frac{1}{3} }} \right.
a_2=-27*(- \frac{1}{3} )=9, a_3=-27* \frac{1}{9}=-3, a_4=-27*(- \frac{1}{27} )=1
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
marusia20022 marusia20022  08.06.2019 05:30
X-y=5 2x+3y=-25 как решить методом подстоновки...
lizstys lizstys  08.06.2019 05:30
Преобразуйте в многочлен выражение: (1-2y)^2-4y(1+y)...
Darya4567 Darya4567  08.06.2019 05:30
Найдите наибольшее значение функции y=-4sin(3x-7)+1...
loooollik loooollik  08.06.2019 05:30
Под корнем 4х+32 деленное на 7, равно 6...
масяня155 масяня155  08.06.2019 05:30
Впараллелограмме авсд ав=16 см, ве и вк- соответственно высоты, проведенные к сторонам ад и сд. угол евк = 60гр.определите длину высоты ве...
brankjs brankjs  23.06.2020 15:17
Lg(2X)=1+2lg7 решить уравнение...
valeriyait valeriyait  22.06.2020 15:19
2. Найти все первообразные функции: f(x) = 8e4x-3 + 3 + 5. 3х5 – 2x – 7....
seal2004 seal2004  30.03.2020 13:58
Площа круга дорівнює 22 см2 . Обчисли радіус кола....
Доминика671554 Доминика671554  30.03.2020 13:57
Користуючись теоремою, оберненою до теореми Вієта визначте корені рівняння:1) x²+5x-14=0;2)x²+11x+30;...
pya98 pya98  30.03.2020 13:57
Перший член геометричної прогресії є додатним числом. За якого значення знаменника цієї прогресії сума перших трьох її членів набуває найменшого значення?...

Популярные вопросы