1. Алгебра
  2. Четвертый член арифметической

Четвертый член арифметической прогрессии равен 16, а сумма седьмого и десятого 5. найдите сумму первых восемнадцати членов прогрессии полное решение! !

Ірина428 Ірина428    1   03.09.2019 01:20    1

Ответы
owl42 owl42  06.10.2020 13:36

Член арифметической прогрессии (начиная со второго) задаётся формулой:

aₙ = a₁+(n-1)·d,  n = 2, 3, 4, ...

a₁ - первый член прогрессии. d - разность ариф. прог. d =

a₄ = a₁+(4-1)·d = a₁+3d = 16

a₇+a₉ = (a₁+(7-1)·d) + (a₁+(10-1)·d) = a₁+6d+a₁+9d = 2a₁+15d = 5

Составим систему двух уравнений с двумя переменными:

\displaystyle -\left \{ {{a_1+3d=16\;|\cdot 2} \atop {2a_1+15d=5\quad }} \right.\\\\\left \{ {{a_1=16-3d\qquad \qquad \qquad \qquad } \atop {2a_1-2a_1+6d-15d=32-5}} \right. \\\\\left \{ {{d=\dfrac{27}{-9}=-3\qquad \qquad } \atop {a_1=16-3\cdot (-3)=25}} \right.

Сумма первых n членов ариф. прог. вычисляется по формуле:

S_n=\d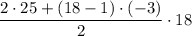frac{a_1+a_n}{2} \cdot n=\dfrac{a_1+a_1+(n-1)\cdot d}{2}\cdot n=\\\\=\dfrac{2a_1+(n-1)\cdot d}{2} \cdot n

S₁₈ = \dfrac{2\cdot 25+(18-1)\cdot (-3)}{2} \cdot 18 = (50-3·17)·9 = (50-51)·9 = -1·9 = -9

ответ: -9.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
minikolp12344 minikolp12344  16.07.2019 04:20
Многочлен к стандартному виду и запишите его в порядке убывания степеней переменной: 10b^2+b^3-4b^2+1-3b+5...
AndreevaAS2 AndreevaAS2  16.07.2019 04:20
Последовательность -16; -13; является...
DianaBanana777 DianaBanana777  16.07.2019 04:20
Разложите многочлен на множители 1)x^6+y^6 2)(a-b)^3+b^3 выполните действия (n+1/2)(n^2-1/2n+1/4)...
alina17anilaalina alina17anilaalina  16.07.2019 04:20
Найдите корни уравнения -20x^2+300x=0...
DemonOfFood DemonOfFood  16.07.2019 04:20
Квадрат суммы двух последовательных натуральных чисел больше суммы их квадратов на 612.найдите эти числа...
dashenkanosova5 dashenkanosova5  29.06.2019 22:40
Разложите на множители (a²b-ab²) 9x-x³...
даша2816 даша2816  29.06.2019 22:40
Преобразовав линейное уравнение 4x+5y-11=0 к виду линейной функции y=kx+m найдите ее угловой кллэффициент...
dassshaVv dassshaVv  29.06.2019 22:40
Для экскурсии нужно собрать деньги. если каждый экскурсант принесёт по 120 тенге, то на расходы не хватит 360 тенге, а если каждый внесет по 140 тенге, то останется 360 тенге. сколько...
Оля11111110 Оля11111110  29.06.2019 22:40
Разложить на множите 5a^2-25ab 2c+2c^2-d-ad...
ulaklimenko49 ulaklimenko49  29.06.2019 22:40
Решите неравенство 5-2x 3(1-x)-12x...

Популярные вопросы