Через 2 ч после выезда с фабрики шофер посмотрел на спидометр и заметил, что проехал только 112 км. Он прикинул мысленно, что если и дальше поедет с той же скоростью, то на 30 мин опоздает с доставкой груза на станцию. Поэтому шофер увеличил скорость и прибыл на станцию даже на 30 мин раньше срока. Определить начальную и последующую скорости движения автомобиля, если расстояние от фабрики до станции по спидометру составляет 280 км. Первоначальная скорость км\ч. Значить после того, как шофёр ускорился x - км\ч, скорость стала (56 + x) км\ч. Так же из условия следует, что он приехал на 30 мин. ==> 0,5 ч. раньше. Хотя так же дана информация, что, если он будет ехать с первоначальной скоростью, то он опоздает на 0,5 ч.
путь по спидометру 280 км, но т.к. первоначальная скорость, с которой шофёр ехал 112 км, нам известна, то, получается, что оставшаяся часть пути 280 - 112 = 168 км он проехал со скоростью 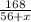км\ч. А как составить уравнение для нахождения скорости, да ещё, по условию, скоростей я не знаю(

Ddf001    1   12.08.2021 11:41    6