1. Алгебра
  2. Цена товара была дважды

Цена товара была дважды снижена на одно и то же число процентов. на сколько процентов снижалась цена товара каждый раз, если его первоначальная стоимость 400 рублей, а окончательная 256.?

GIRLENKA GIRLENKA    1   03.03.2019 12:40    4

Ответы
shybite shybite  06.06.2020 21:54

Пусть х % от цены составляло её изменение, тогда стоимость товара после первого изменения была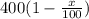 400(1-\frac{x}{100}), а после второго -

400(1-\frac{x}{100})(1-\frac{x}{100}) или 256 рублей. Составим и решим уравнение:

 

400(1-\frac{x}{100})(1-\frac{x}{100})=256

 

(\frac{100-x}{100})^2=\frac{256}{400}

 

10000-200x+x^2=\frac{16\cdot10000}{25}

 

10000-200x+x^2=6400

 

x^2-200x+10000-6400=0

 

x^2-200x+3600=0

 

по теореме Виета:

x_1=20 и x_2=180100(не подходит)

 

ответ: цена товара каждый раз снижалась на 20 %.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
myster2 myster2  22.08.2019 10:40
Разложите на множители: 27c^3-d^3+9c^2+3cd+d^2...
Natasha2910 Natasha2910  23.09.2019 11:50
1) решите уравнение 3x^2-x=0; 2) решите уравнение 2x^3+x^2-8x-4=0...
Apelsin2403 Apelsin2403  23.09.2019 11:50
Сложите уравнение по формуле сокращенного умножения : х^2-6х+9=...
kulikovamascha kulikovamascha  23.09.2019 11:50
Один из углов прямоугольного треугольника равен 60 а сумма гипатинузы и меньшего катета = 45 см найти гипотинузу...
West31 West31  23.09.2019 11:50
Объясните , как их я почти месяц болею , мне контрольную домой передали , а как это всё делать я не 2х²-5х³-6х+15...
агата281 агата281  10.09.2020 10:59
Какое из выражений удобнее для вычисления его значения :ax+bx или ( a+b)x​...
almirashagieva almirashagieva  10.09.2020 10:53
Упростить выражение (3a-2b)*(2a+b)-6*(a+b)²​...
alizhanayanaoxi717 alizhanayanaoxi717  29.11.2021 02:50
Составить график функции y = 1,8x...
Спасибо181 Спасибо181  29.11.2021 03:02
Найдите значение выражения -9x^3 при x= -1/3...
AhhaYakovkeva AhhaYakovkeva  29.11.2021 03:03
, кто может . последовательность заданной формулой An n+4|2 a)Записать пять первых членов послед-ти а1; а2; а3; а4;а5 b)Найти сумму десяти первых чисел последовательности....

Популярные вопросы