CB−→−⋅CF−→= ;
2. OF−→⋅OA−→−= ;
3. AB−→−⋅AF−→
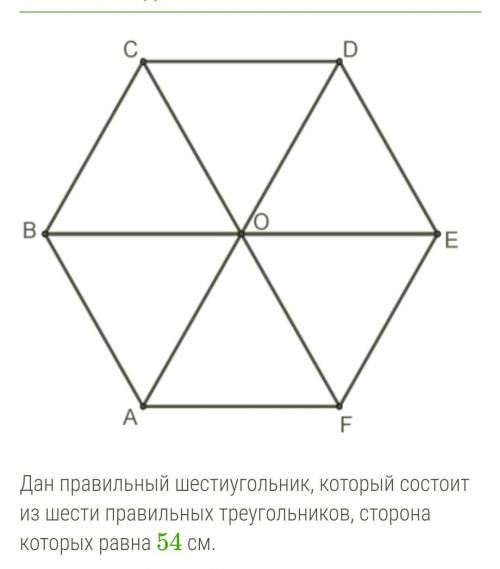
Другие вопросы по теме Алгебра
Популярные вопросы
- прикметники при творенні яких відбувається чергування приголосних звуків 1слабкий.2дужий3великий4близький5низький...
1 - Как обозначить корень в русскому языке...
3 - Поясніть, чому в дослiдi тиск повітря у трубці зростає під час опускання її...
3 - Гипертекст - это: 1)Текст очень большого размера 2)Текст, в котором используется...
3 - Какие были особенности ГУЛАГа?...
2 - Конспект електрычного струму едыныця напруги вольтметр...
1 - Виділіть безсполучникове складення речення. А. Через єдине невеличке віконце...
3 - Почему Карл первый не стал монахом...
3 - Тип Назваприродної зониГеографічнеположенняОсобливостікліматугрунтівРослинний...
2 - Expressing opinions 7.53Use the adjectives to discuss TVprogrammes, as in the...
3
1. CB−→ ⋅ CF−→ = ?
Для решения этой задачи нам нужно найти скалярное произведение векторов CB−→ и CF−→. Но прежде всего давай определим, что такое скалярное произведение.
Скалярное произведение двух векторов определяется следующим образом:
AB−→ ⋅ CD−→ = |AB−→| ⋅ |CD−→| ⋅ cosθ,
где |AB−→|, |CD−→| - это длины векторов AB−→ и CD−→ соответственно, а cosθ - это косинус угла между векторами AB−→ и CD−→.
Итак, применяем формулу скалярного произведения:
CB−→ ⋅ CF−→ = |CB−→| ⋅ |CF−→| ⋅ cosθ.
Однако, нам не даны значения длин векторов, поэтому мы не можем точно вычислить значение скалярного произведения. Здесь требуется дополнительная информация.
2. OF−→ ⋅ OA−→ = ?
Аналогично, мы должны использовать формулу скалярного произведения:
OF−→ ⋅ OA−→ = |OF−→| ⋅ |OA−→| ⋅ cosθ.
Но, как и в предыдущем задании, нам не даны значения длин векторов, поэтому мы не можем точно вычислить значение скалярного произведения. Здесь также требуется дополнительная информация.
3. AB−→ ⋅ AF−→ = ?
Для решения этой задачи нам нужно найти скалярное произведение векторов AB−→ и AF−→.
Применим формулу скалярного произведения:
AB−→ ⋅ AF−→ = |AB−→| ⋅ |AF−→| ⋅ cosθ.
У нас даны координаты векторов AB−→ и AF−→, поэтому мы можем вычислить значения этих векторов и использовать их для вычисления скалярного произведения. Пусть координаты точек A и B даны как (x1, y1) и (x2, y2) соответственно, а координаты точек A и F даны как (x3, y3) и (x4, y4) соответственно.
Тогда вектор AB−→ = (x2 - x1, y2 - y1) и вектор AF−→ = (x4 - x3, y4 - y3).
Теперь мы можем вычислить значения длин векторов |AB−→| и |AF−→|, а также косинус угла между ними cosθ, и затем подставить эти значения в формулу для вычисления скалярного произведения.
Итак, решая задачу пошагово, мы сначала найдем векторы AB−→ и AF−→:
AB−→ = (x2 - x1, y2 - y1),
AF−→ = (x4 - x3, y4 - y3).
Затем вычислим длины векторов |AB−→| и |AF−→|, используя формулу для длины вектора:
|AB−→| = √((x2 - x1)^2 + (y2 - y1)^2),
|AF−→| = √((x4 - x3)^2 + (y4 - y3)^2).
И, наконец, вычислим косинус угла между векторами AB−→ и AF−→, используя формулу для косинуса угла между векторами:
cosθ = (AB−→⋅AF−→) / (|AB−→|⋅|AF−→|).
Подставляем значения в формулу скалярного произведения и получаем окончательный ответ.
Обратите внимание, что для того, чтобы точно решить задачу, нам нужно знать значения координат точек A, B и F. Если эта информация задана, мы можем вычислить скалярное произведение векторов AB−→ и AF−→ с помощью указанных выше шагов. Если эта информация не задана, решить задачу точно нельзя.